Question

Радіус основи конуса відноситься до твірної, як 4 : 5, а висота конуса дорівнює 6 см. Знайдіть площу бічної поверхні конуса.

Answer 1

Ответ:

Sбок. = 80π (см²)

Объяснение:

Радиус основания конуса относится к образующей, как 4 : 5, а высота конуса равна 6 см. Найдите площадь боковой поверхности конуса.

Дано:

Конус

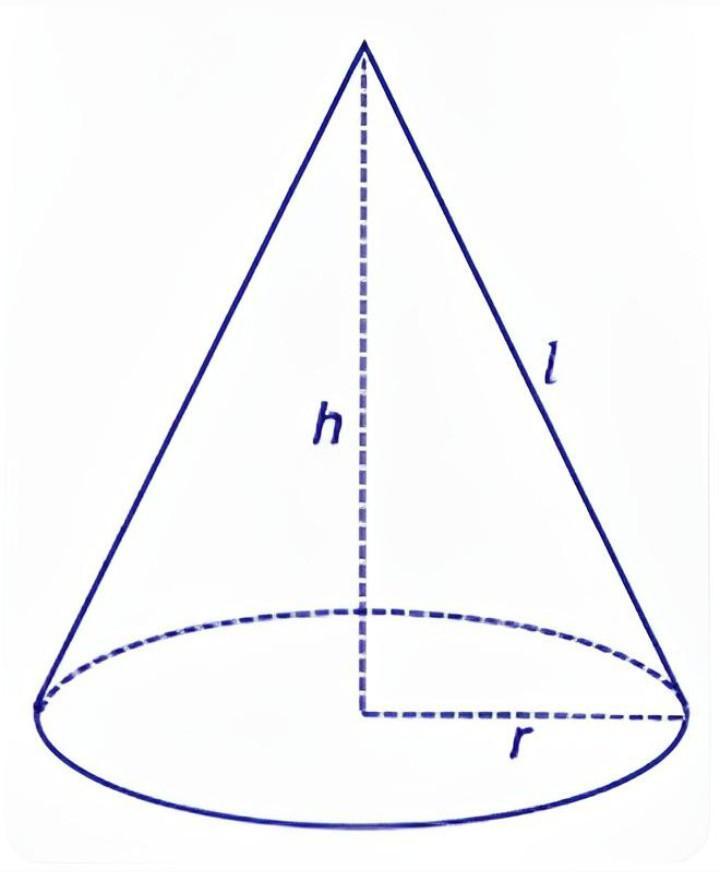
h = 6 см - высота

r : l = 4 : 5

Найти:

Sбок.

Решение:

Пусть x - коэффициент пропорциональности , тогда r = 4x , l = 5x . В пользу того, что высота ,радиус основания и образующая конуса образуют прямоугольный треугольник , то по т.Пифагора:

6² + (4х)² = (5х)²

36 + 16х² = 25х²

25х² - 16х² = 36

9х² = 36| : 9

х² = 4

х$_{1,2}= \pm \sqrt{4} = \pm 2$

Отрицательное значение не подходит по условию задачи , то есть х = 2.

Значит, r = 4x = 4·2 = 8 (см) ; l = 5x = 5·2 = 10 (см)

Находим площадь боковой поверхности по формуле:

Sбок. = πrl

Следовательно:

Sбок. = π·8·10 = 80π (см²)