Question

Дано: ABCD - квадрат,
BF 1 (ABC), BF = 4, AC = 6.
Найдите SAcF:

Answer 1

Ответ:

AF/BF=AC/AB

AF=BF=1

AF=BF=4

CF=AF•BC/AB=4•6/6=4

SF=4

AF=4

AC=6

SAcF=(1/2)•AF•SC=(1/2)•4•6=12

ответ:SAcF=12

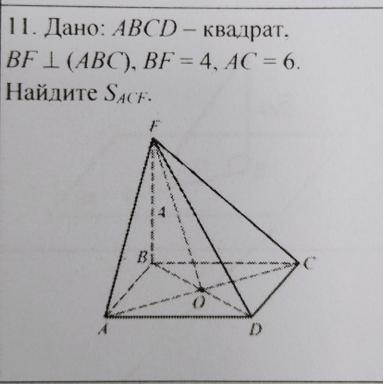
Дано: ABCD - квадрат,

BF 1 (ABC), BF = 4, AC = 6.

Найдите SAcF:

Чтобы найти площадь треугольника SAcF, необходимо знать длины сторон треугольника.треугольник SAcF есть прямоугольный, потому что один из его углов (угол S) = 90°(в силу того, что SF является высотой квадрата ABCD, а угол ASF прямой).За т.Пифагора находим АF:

AF^2 = AC^2 - CF^2

треугольник SAcF подобен треугольнику SBF (они имеют два равных угла), отношение длин сторон треугольников равно отношению соответствующих сторон квадрата ABCD:

AF / BF = AC / AB

AB = AC,ABCD - квадрат,имеем:

AF / BF = 1

AF = BF = 4

Найдем CF,( треугольники BCF и BAF равны,они имеют два равных угла и общую сторону BF),имеем:

CF = AF * BC / AB = 4 * 6 / 6 = 4

Длины сторон треугольника SAcF равны: SF = 4 (по условию), AF = 4, AC = 6:

SAcF = (1/2) * AF * SC = (1/2) * 4 * 6 = 12

Ответ: SAcF = 12.