Question

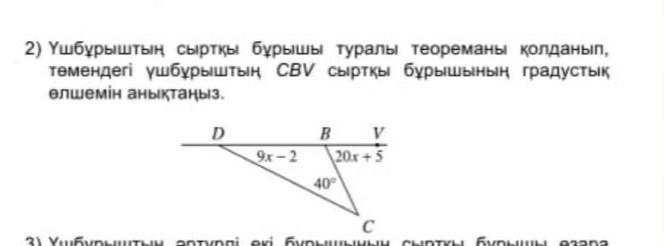
Используя теорему о внешнем угле /\-ТРЕУГОЛЬНИка определить внешнего угла СВV окружности находящееся внизу​

Answer 1

Ответ:

x=3

∠BDC=25°

∠VBC=65°

Объяснение:

∠VBC=∠BCD+∠BDC;

Внешний угол треугольника равен сумме двух внутренних углов треугольника не смежных с ним.

Уравнение:

20х+5=9х-2+40

20х-9х=40-2-5

11х=33

х=3

∠ВDC=9x-2=9*3-2=25°

∠VBC=20x+5=20*3+5=65°