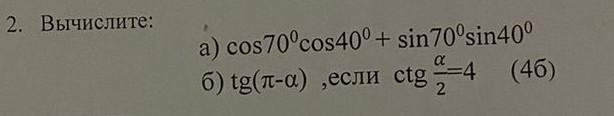Question

a) cos70°cos40º + sin70°sin40°
б) tg (π-a), если ctg а/2=4 ​

Answer 1

Ответ:

Объяснение:

A)

Мы можем воспользоваться формулой для косинуса суммы двух углов:

cos (α + β) = cos α cos β - sin α sin β

Здесь α = 70°, а β = 40°, поэтому мы можем записать:

cos 70° cos 40° + sin 70° sin 40° = cos (70° - 40°) = cos 30° = √3 / 2

Таким образом, исходное выражение равно √3 / 2.

B)

Мы можем воспользоваться тригонометрической формулой для тангенса разности двух углов:

tg (π - α) = -tg α

Также нам дано, что:

ctg α/2 = 4

Нам нужно выразить tg α через ctg α/2. Для этого мы можем воспользоваться формулами связывающими различные тригонометрические функции:

ctg α/2 = 1 / tg α/2 = 2 / (tg α + cotg α) = 4

Подставляем это выражение во вторую формулу:

4 = 2 / (tg α + 1 / tg α)

Умножаем обе части на (tg α)^2:

4(tg α)^2 = 2(tg α)^2 + 2

Выражаем (tg α)^2:

2(tg α)^2 = 2

(tg α)^2 = 1

tg α = ±1

Таким образом, tg (π - α) = -tg α = -1.