Question

Найдите площадь поверхности и объем куба, если а=3х+2у помогите

Answer 1

Ответ:

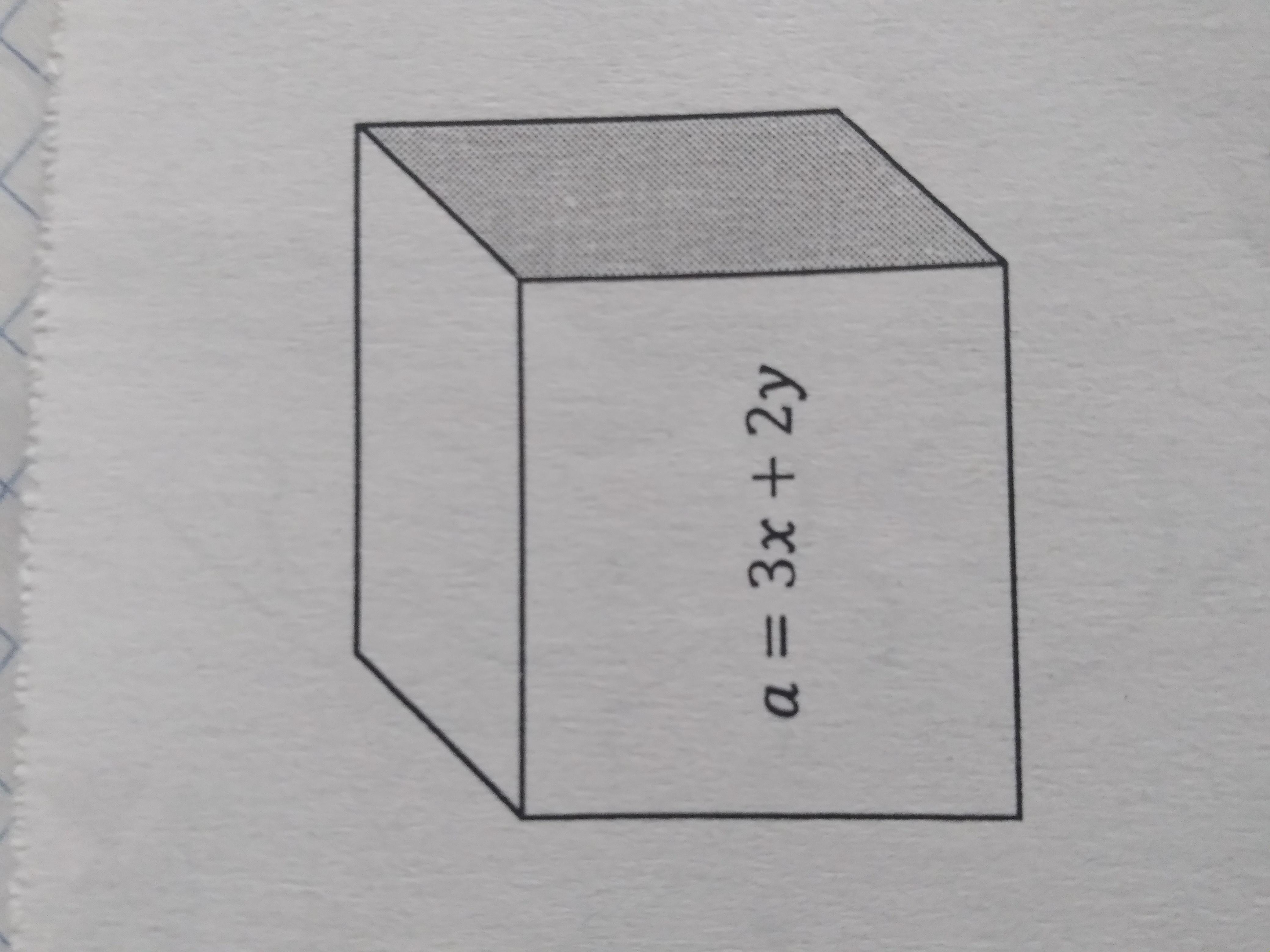
Для того чтобы найти площадь поверхности куба и его объем, нам нужно знать длину его стороны. Для этого нам дано выражение для стороны куба:

a = 3x + 2y

Так как все стороны куба равны, то длина каждой стороны равна a.

Теперь мы можем найти площадь поверхности куба, используя формулу:

S = 6a^2

Заменяя a на 3x + 2y, получим:

S = 6(3x + 2y)^2

S = 6(9x^2 + 12xy + 4y^2)

S = 54x^2 + 72xy + 24y^2

Таким образом, площадь поверхности куба равна 54x^2 + 72xy + 24y^2.

Чтобы найти объем куба, мы используем формулу:

V = a^3

Заменяя a на 3x + 2y, получим:

V = (3x + 2y)^3

V = 27x^3 + 54x^2y + 36xy^2 + 8y^3

Таким образом, объем куба равен 27x^3 + 54x^2y + 36xy^2 + 8y^3.