Question

Помогите!Просто ответ
В основании четырехугольной пирамиды лежит ромб со стороной 18 см и острым угом 60. Высота пирамиды проходит через точку пересечения
диагоналей ромба и равна 12 ом. Найди площадь боковой поверхности
данной пирамиды.

Answer 1

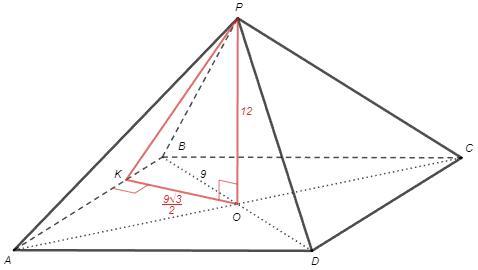
OK⊥AB, PO⊥(ABC) => PK⊥AB (т о трех перп)

BO=9 ; ∠ABO=60

OK =9 sin60 =9√3/2

PK =√(PO^2+OK^2) =√(144 +27/4) =3√91/2

S(APB) =1/2 AB PK =18*3√91/2*2

Рассотяния от O до сторон равны

=> высоты боковых граней равны (т Пифагора)

=> площади боковых граней равны

Sбок =4 S(APB) =18*3√91 =54√91 (см^2)