Question

Через вершину В рівностороннього трикутника АВС до його площини провели перпендикуляр DB довжиною 4 корінь із 3
см. Знайти кут між прямою AD та площиною трикутника, якщо його площа дорівнює 4 корінь із 3 см2.​

Answer 1

Ответ:

60°

Объяснение:

//////////////////////////////////////

Answer 2

Ответ:

Угол между прямой AD и плоскостью треугольника равна 60°.

Объяснение:

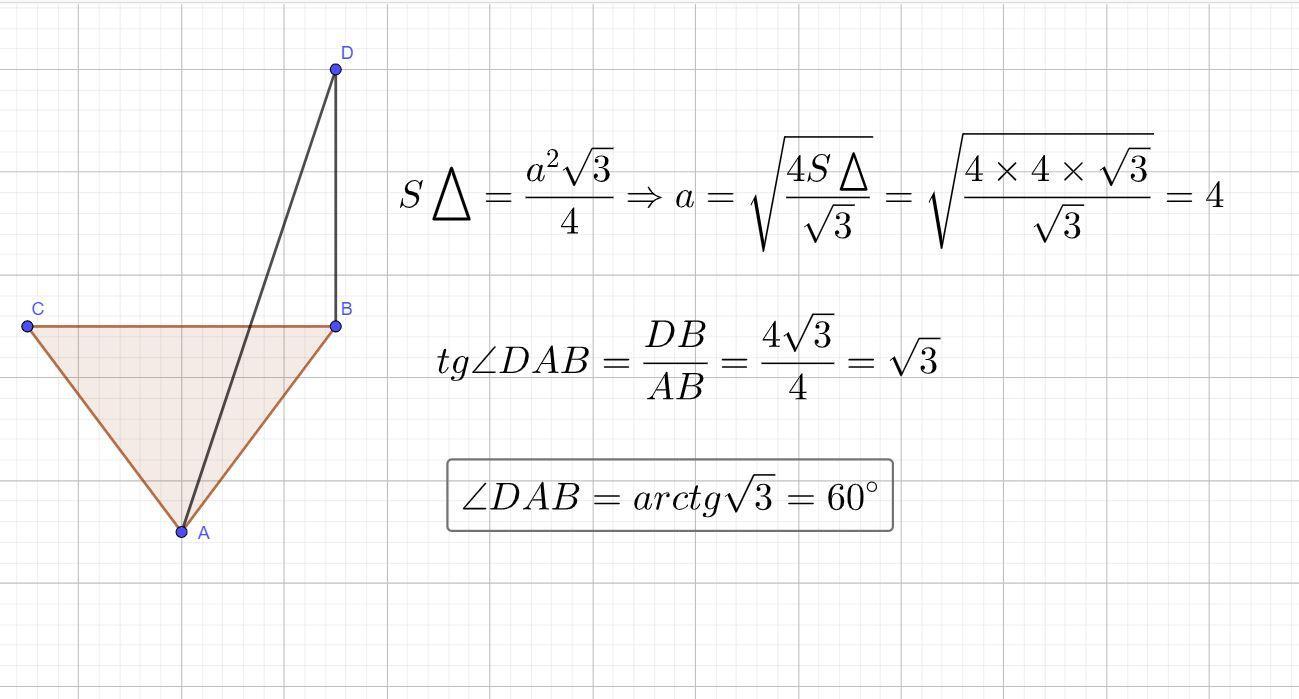
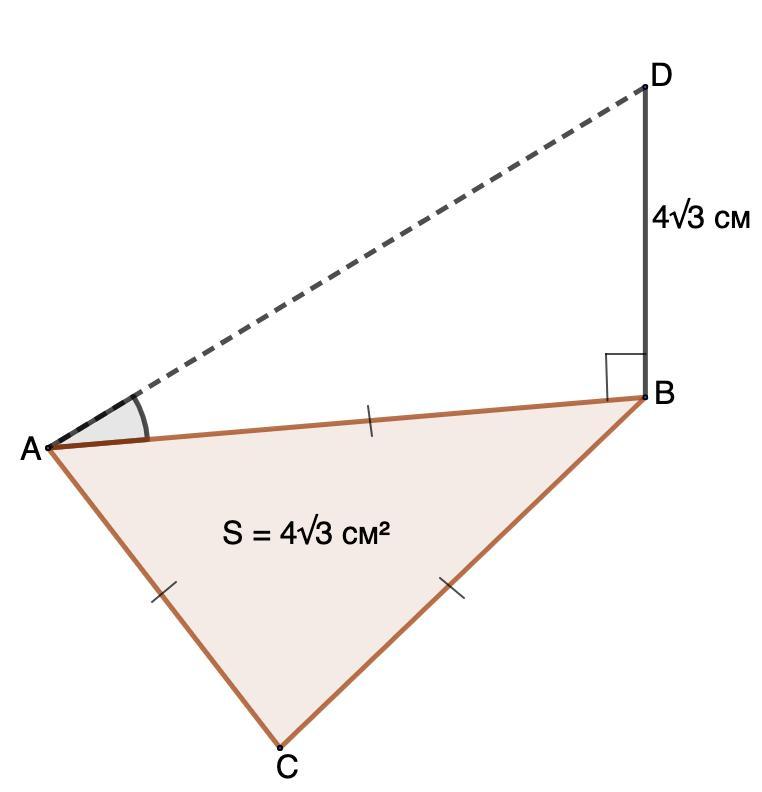
Через вершину В равностороннего треугольника АВС к его плоскости провели перпендикуляр DB длиной 4√3 см. Найти угол между прямой AD и плоскостью треугольника, если его площадь равна 4√3 см².​

Дано: ΔАВС - равносторонний;

BD ⊥ (АВС); BD = 4√3 см;

S(ABC) = 4√3 см²

Найти: угол между прямой AD и плоскостью треугольника.

Решение:

• Угол между прямой и плоскостью - угол между прямой и ее проекцией на данную плоскость.

BD ⊥ (АВС) ⇒ АВ - проекция AD на (АВС)

⇒ Искомый угол DAB.

• Формула площади равностороннего треугольника:

                                      $\displaystyle \bf S=\frac{a\sqrt{3} }{4}$  ,

где а - сторона треугольника.

Подставим данные значения и найдем сторону треугольника:

$\displaystyle \bf 4\sqrt{3}=\frac{a^2\sqrt{3} }{4}\;\;\;\;\;|\cdot\frac{4}{\sqrt{3} } \\ \\16 =a^2\\\\a=4\;_{(CM)}$

Рассмотрим ΔADB - прямоугольный.

• Тангенс угла - отношение противолежащего катета к прилежащему.

$\displaystyle \bf tg\angle DAB=\frac{DB}{AB}=\frac{4\sqrt{3} }{4}=\sqrt{3}$

⇒  DAB = 60°

Угол между прямой AD и плоскостью треугольника равна 60°.