Пряма дотикається до кола із центром О в точці С. На дотичній по різні боки від точки С позначили точки А і В такі, що СА = СВ. Знайдіть відрізок ОА, якщо OB=9 см.
Ответы
Ответ дал:
3
Для розв'язання цієї задачі ми можемо скористатися властивістю, що кут між дотичною до кола і відрізком, що його кінець лежить на колі, є прямим кутом. Оскільки точки А і В знаходяться на дотичній, то СА і СВ є дотичними до кола, а кути ОСА і ОВС є прямими кутами.
Оскільки СА = СВ, то кути ОСА і ОСВ є рівними, тому ОС є бісектрисою кута АОВ. Отже, ми можемо використати теорему про бісектрису, щоб знайти довжину відрізка ОА:
OA/OB = SA/SB
Оскільки СА = СВ, то SA = SB, тому:
OA/9 = SA/SA
OA = 9
Отже, відрізок ОА має довжину 9 см.
Оскільки СА = СВ, то кути ОСА і ОСВ є рівними, тому ОС є бісектрисою кута АОВ. Отже, ми можемо використати теорему про бісектрису, щоб знайти довжину відрізка ОА:
OA/OB = SA/SB
Оскільки СА = СВ, то SA = SB, тому:
OA/9 = SA/SA
OA = 9
Отже, відрізок ОА має довжину 9 см.
Приложения:
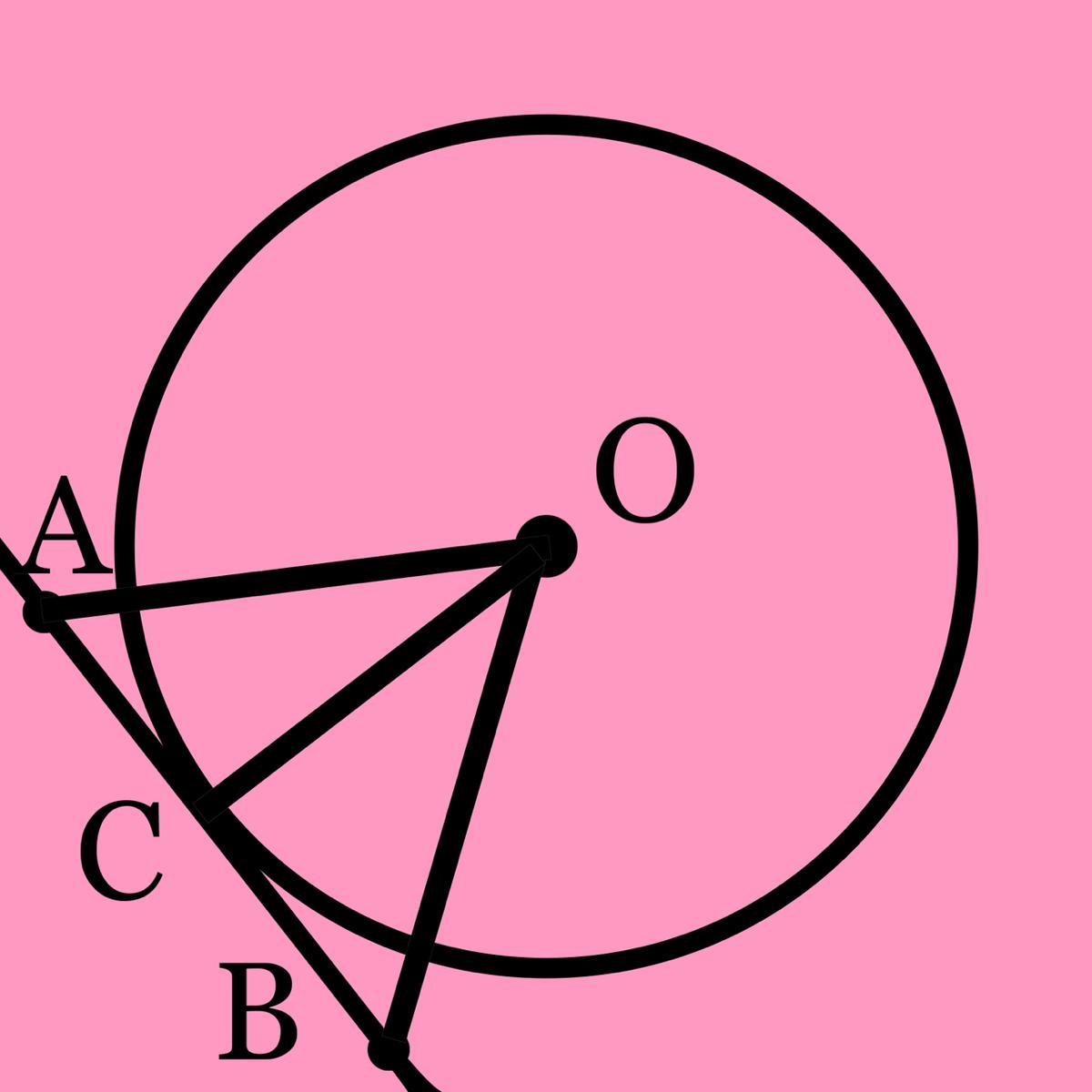
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад