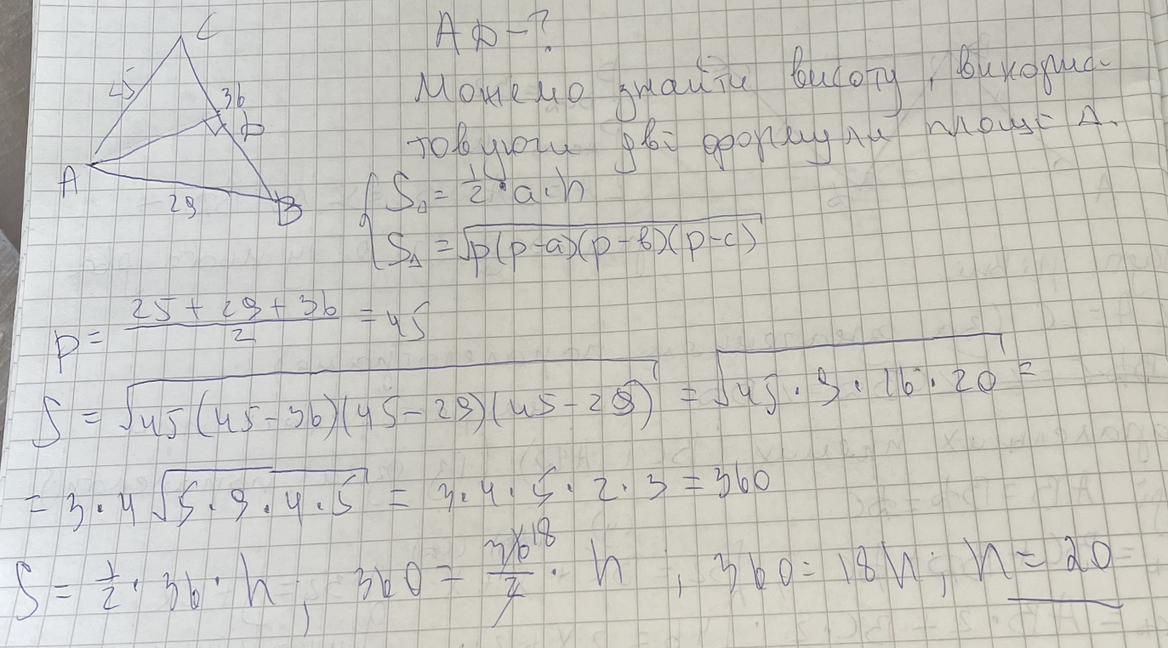557. Стороны треугольника равны 36 см, 29 см и 25 см. Найдите
высоту треугольника, проведенную к большей стороне.

Ответы
Ответ:
Задача досить складна. Уважно читай пояснення, там важливі деталі.
Объяснение:
Задача заключается в нахождении высоты треугольника, опущенной на наибольшую сторону, используя длины сторон. Для решения этой задачи мы можем воспользоваться теоремой Пифагора, которая гласит, что в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Мы знаем длины сторон треугольника, поэтому можем определить, какая из сторон является наибольшей, используя метод сравнения. Допустим, что сторона 36 см - наибольшая. Затем мы можем построить высоту, опущенную на эту сторону, так что она будет перпендикулярна к этой стороне и проходит через ее середину.
Чтобы построить высоту, мы можем взять середину стороны 36 см и соединить ее с вершиной, противолежащей этой стороне (то есть соединить вершину с серединой стороны 36 см). Затем мы получим прямоугольный треугольник с гипотенузой 36 см, одним катетом 14,5 см (половина 29 см) и другим катетом - искомой высотой h.
Применяя теорему Пифагора, мы можем найти длину высоты:
h^2 = 36^2 - (14.5)^2
h^2 = 1296 - 210.25
h^2 = 1085.75
h =(1085.75)
h ≈ 32.97 см
Таким образом, мы получили высоту треугольника, проведенную к большей стороне, равную приблизительно 32.97 см.