Question

N 8: помогите пожалуйста

Answer 1

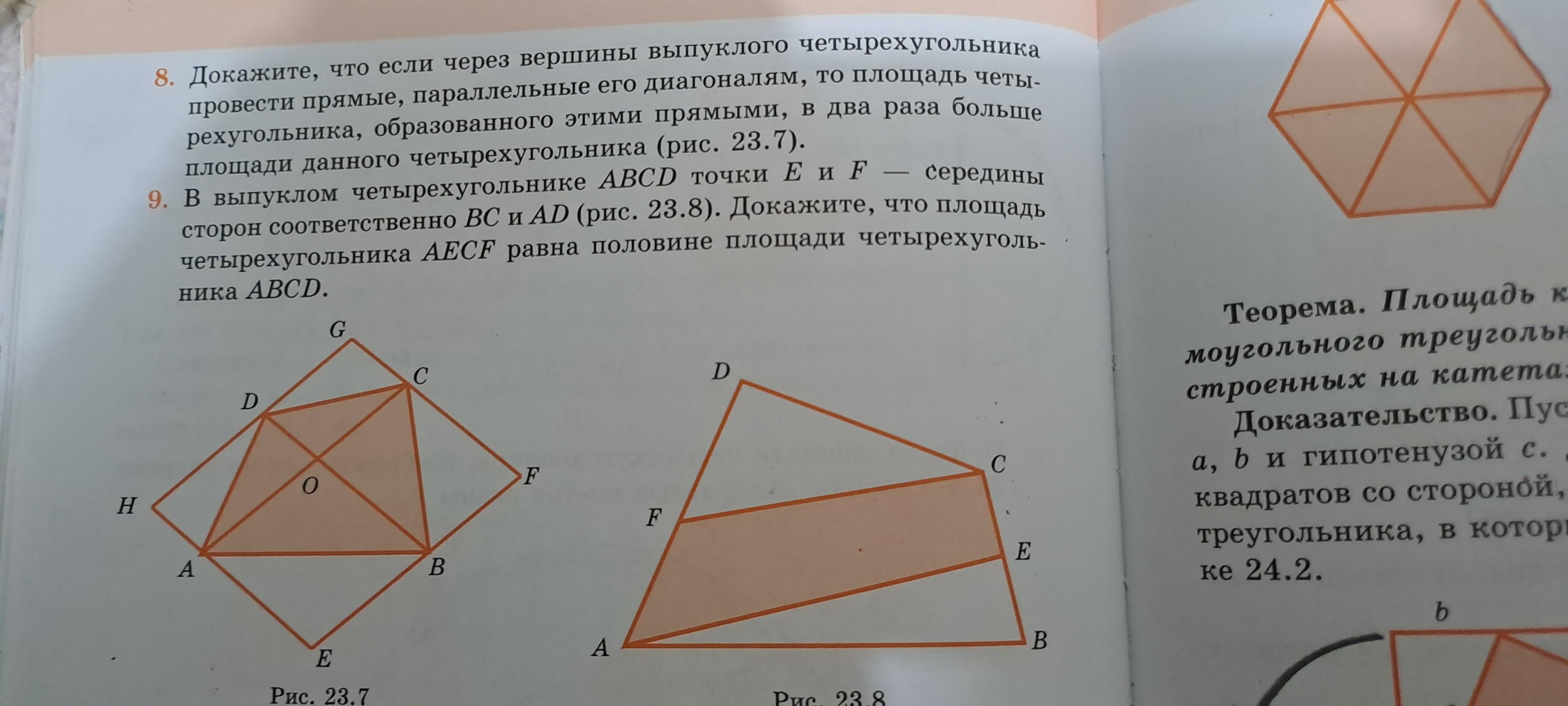
Докажите, что если через вершины выпуклого четырехугольника провести прямые, параллельные его диагоналям, то площадь четырехугольника, образованного этими прямыми, два раза больше площади данного четырехугольника

Решение.

1) По условию АС||НG.

Также НА||DO, GC|DO => HA||GC. Значит АНGС- параллелограмм, тк противоположные стороны попарно параллельны.

S( AHGC) =AC•h1=2•(1/2•AC• h1) =

=2• S(ADC).

2) По условию EF||AC. Tакже EА||BO, FC||BO => EA|FC. Значит EАCF- параллелограмм, тк противоположные стороны попарно параллельны.

S( EACF) =AC•h2=2•(1/2•AC• h2) =

=2• S(ABC).

3) S( EHGF)= S( AHGC)+S( EACF) = =2•S(ADC)+2•S(ABC)=

=2•(S(ADC)+S(ABC)) =2•S(ABCD)