Question

Площа круга, описаного навколо квадрата, дорівнює 128π см2. Знайдіть площу квадрата.

Answer 1

Ответ:

Площадь квадрата равна 256 квадратных сантиметров

Объяснение:

Перевод: Площадь круга, описанного вокруг квадрата, равна 128π см². Найдите площадь квадрата.

Из формулы площади описанного круга найдем R-радиус :

S = πR²

$R = \sqrt{ \frac{S}{\pi} } = \sqrt{ \frac{128\pi}{\pi} } = \sqrt{128} = 8 \sqrt{2} (cm)$

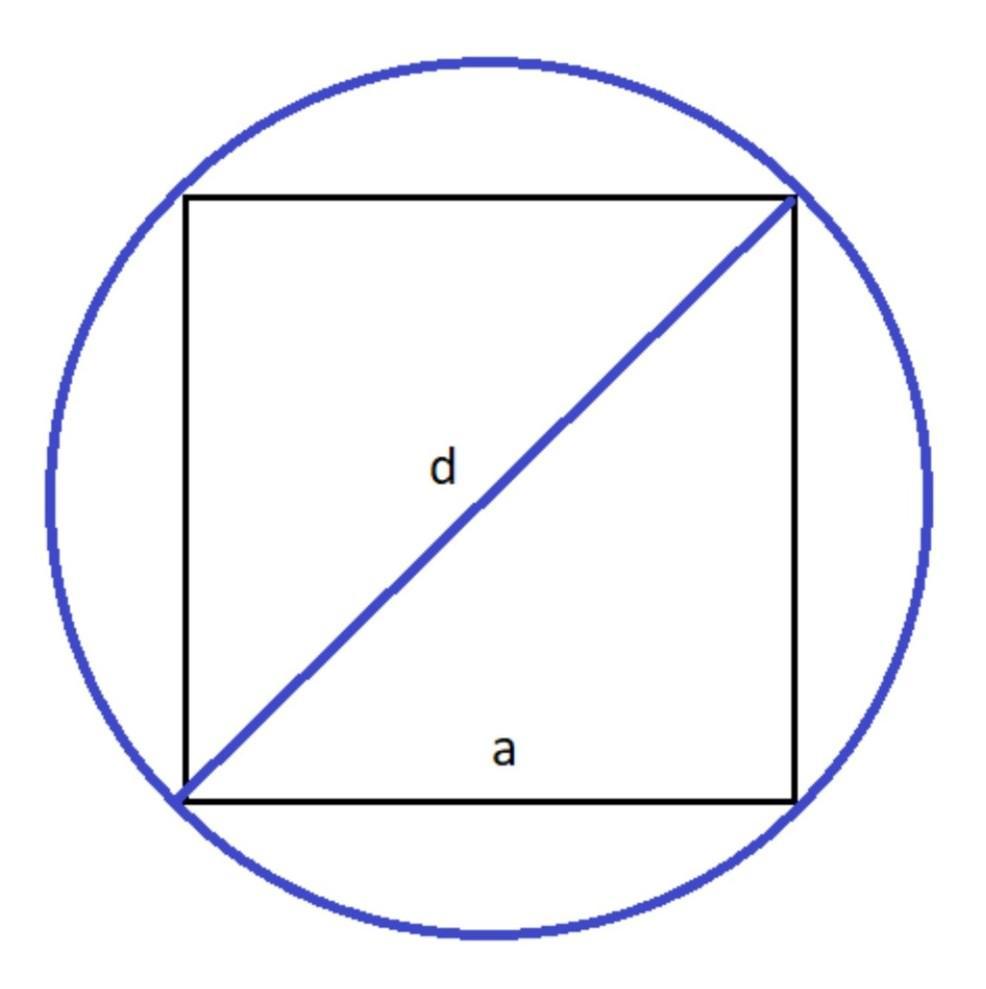
Диаметр описанной около квадрата окружности будет совпадать с диагональю квадрата , тогда найдем диаметр :

D = 2R = 2·8√2 = 16√2 (см)

Значит , d кв. = 16√2 (см)

Найдем площадь квадрата по формуле S = d²/2 :

S = (16√2)²/2 = 512/2 = 256 (см²)

#SPJ1