Question

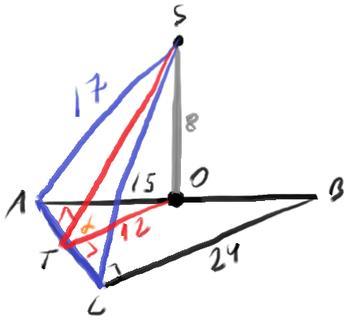
В основании треугольной пирамиды SABC лежит прямоугольный треугольник ABC с прямым углом C. Основание высоты SO этой пирамиды является серединой ребра AB.
а) Докажите, что SA = SC.

б) Найдите угол между плоскостями SAC и ABC, если AB = 30, SC = 17, СB = 24.

Answer 1

Середина гипотенузы - центр описанной окружности.

Если вершина пирамиды падает в центр описанной окружности основания, то боковые ребра равны (SA=SC) и образуют с основанием равные углы.

(OA=OC, SO⊥OA, SO⊥OC, △SAO=△SCO по двум катетам)

Угол между плоскостями - угол между перпендикулярами к общей прямой.

OT⊥AC, SO⊥(ABC) => ST⊥AC (т о трех перп)

∠STO - искомый

SO =√(SA^2-OA^2) =√(17^2-15^2) =8

OT =BC/2 =12 (OT||BC, средняя линия)

tg(STO) =SO/OT =8/12 =2/3