Question

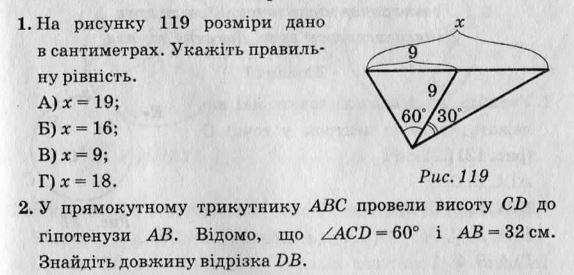
На рисунку 119 розміри дано в сантиметрах. Укажіть правиль-ну рівність.
9
A) x = 19;
60°
30
Б) x = 16;
B) x = 9;
Ґ) x = 18.
Puc. 119
2. У прямокутному трикутнику АВС провели висоту CD до
гіпотенузи АВ. Відомо, що
LACD = 60° i AB = 32 c.
Знайдіть довжину відрізка DB.

Answer 1

Ответ:

Объяснение:

Для розв'язання першого завдання зобразимо на рисунку 119 трикутник АВС з кутом між сторонами АВ та ВС, що дорівнює 60°.

Тоді за теоремою синусів маємо:

x / sin(60°) = 30 / sin(30°)

x = sin(60°) * 30 / sin(30°)

x = √3 * 30 = 30√3

Отже, правильна рівність: x = 30√3.

Для розв'язання другого завдання позначимо точку перетину висоти CD з гіпотенузою AB як точку Е. Оскільки трикутник АВС - прямокутний, то маємо:

AD = AC * sin(60°) = 32 * √3 / 2 = 16√3

CD = AC * cos(60°) = 32 / 2 = 16

DE = AD - AE = 16√3 - AB * sin(60°) = 16√3 - 16 = 16(√3 - 1)

Таким чином, довжина відрізка DB дорівнює:

DB = AB - AD * cos(60°) = 32 - 16√3 / 2 = 32 - 8√3

Отже, відповідь: DB = 32 - 8√3.