Question

ПОМОГИТЕ, ДАЮ 40 БАЛЛОВ!!!
С условием и рисунком, пожалуйста)
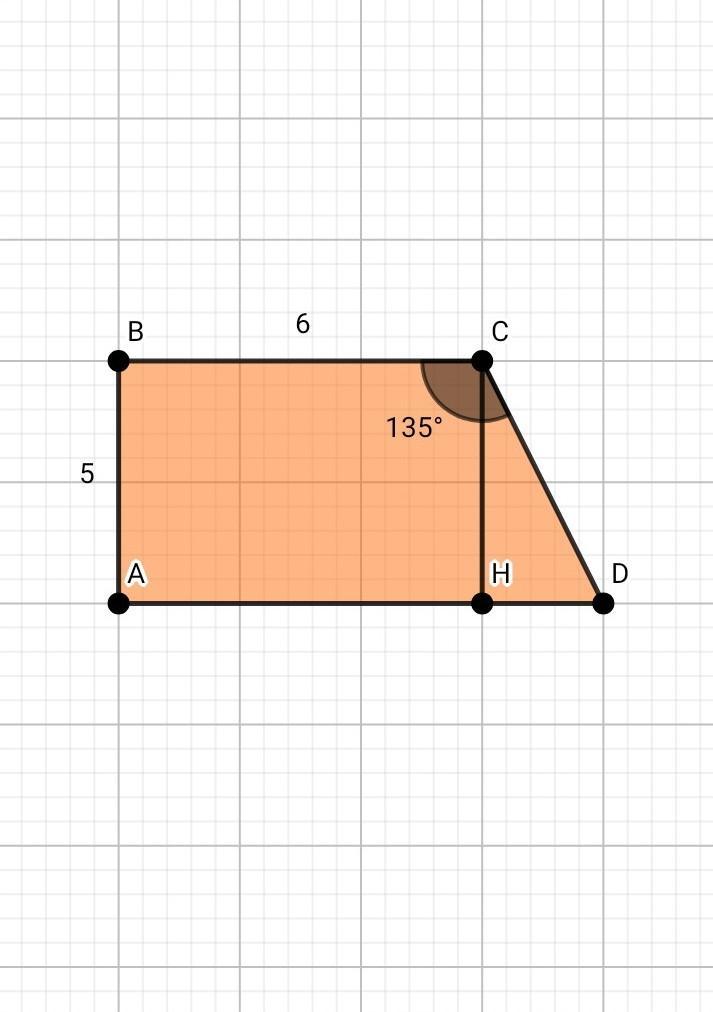
6) У прямокутній трапеції АВСD, BCllAD, AB⊥AD, BC=6см, AB= 5см, ∠BCD=135°. Знайдіть сторони AD i CD трапеції.

Answer 1

Ответ:

AD = 11см, CD = 5√2см

Объяснение:

В прямоугольной трапеции АВСD, BCllAD, AB⊥AD, BC=6см, AB= 5см, ∠BCD=135°. Найдите стороны AD и CD трапеции.

⠀⠀⠀⠀⠀⠀⠀⠀⠀Решение

• Опустим высоту СН. И получим прямоугольник АВСН. АВ = СН = 5см. ВС = АН = 6см.
• Рассмотрим ∆СНD - прямоугольный(СН⟂HD). ∠ВСD = 135°, тогда ∠HCD = 135° - 90° = 45°.
• Косинус угла(HCD) равен отношению прилежащего катета(СН) к гипотенузе(CD).

⠀⠀⠀⠀cos 45° = (CH/CD)

⠀⠀⠀⠀√2/2 = (5/CD)

⠀⠀⠀⠀CD = 10/√2 * √2/√2

⠀⠀⠀⠀CD = 5√2см.

• Найдем HD с помощью Т.Пифагора:

⠀⠀⠀⠀HD = √((5√2)²-5²) = √(50-25) = √25 = 5см

• AH = 6см, HD = 5см, тогда AD = 6 + 5 = 11см

#SPJ1