Question

жестка помогите сочччч у меняя 100 баллов​

Answer 1

Ответ:

120

Объяснение:

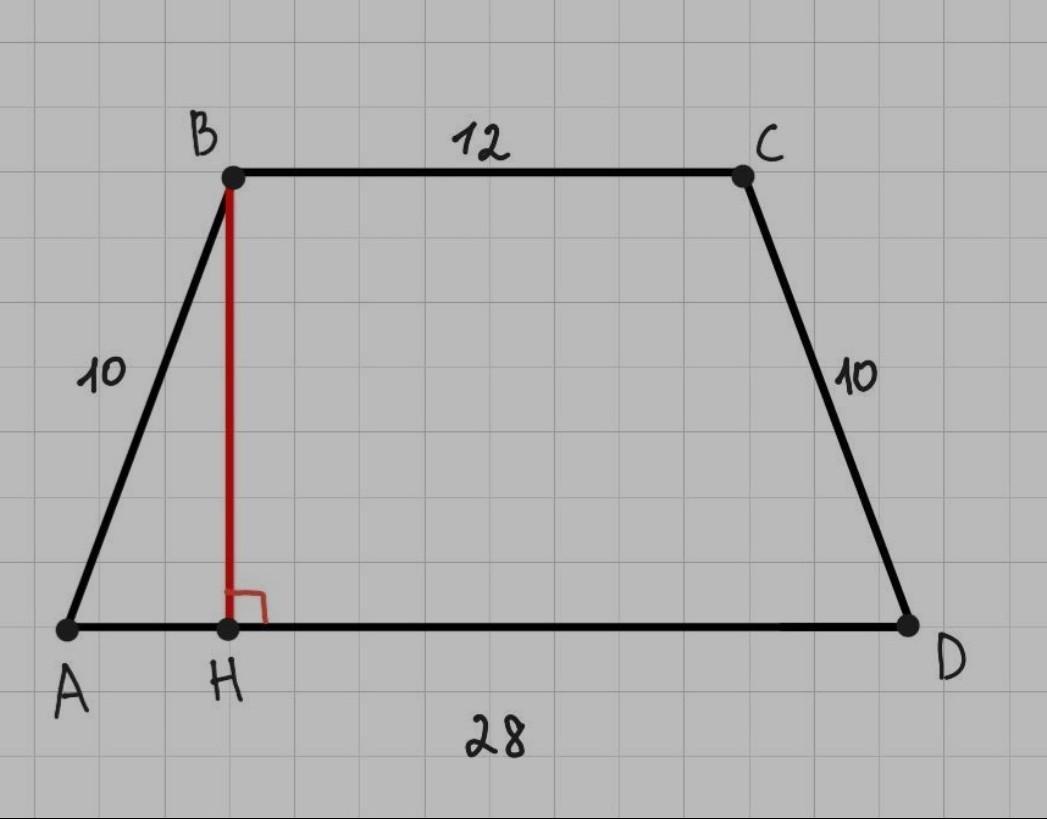
Проведём высоту ВН.

По свойству высоты трапеции, опущенной из вершины на большее основание:

AH=2(AD-BC):

AH=1/2(28-12);

AH= 16/2;

AH=8(см).

В ДАВН (<AHB=90°, т.к. ВН-высота) по т.

Пифагора:

BH²= AB2 - AH²;

BH²= 102 - 82;

BH²=100-64;

BH2=36;

ВН=6 см (6 не подходит).

Высота трапеции ABCD равна 6 см.

Площадь трапеции равна произведению

полусуммы ее оснований на высоту.

S abcd = ½(AD + BC).BH;

s abcd=1/2(12+28)•6;

S abcd=1/240-6;

s abcd=120 (см²).

Answer 2

Відповідь:

S abcd= 640 (см²).

Дано: ABCD — равнобедренная трапеция, BC||AD, BC=12 см, AD=28 см, AB=CD=60 см.

Найти: S трапеции.

Пояснення:

Проведём высоту BH.

По свойству высоты трапеции, опущенной из вершины на бóльшее основание:

 АН = ½(AD–BC);

АН= ½(28–12);

АН= 16/2;

АН= 8 (см).

В ΔАВН (∠АНВ=90°, т.к. ВН—высота) по т. Пифагора:

ВН²= АВ² – АН²;

ВН²= 60² – 8²;

ВН²= 600–64;

ВН²= 536

ВН= 6 см (–6 не подходит).

Высота трапеции ABCD равна 16 см.

Площадь трапеции равна произведению полусуммы ее оснований на высоту.

S abcd = ½(AD + BC)•BH;

S abcd = ½(12+28)•16;

S abcd= ½•40•16;

S abcd= 640 (см²).