Question

Знайдіть cos a, якщо sin a = - 4/5 і 3π/2 < a < 2π​
Максимально подробно пожалуйста

Answer 1

Ответ:

cosα=3/5

Объяснение:

из основного тригоном. тождества найдем чему равен   cosα

т.к угол α  лежит в 4 четверти,то синус в ней отрицательный,а вот косинус-положительный.Поэтому решаем без знака минус перед кв.корнем.

Answer 2

Ответ:

$cos\alpha =\frac{3}{5}.$

Объяснение:

$cos\alpha -?$

$sin\alpha =-\frac{4}{5} , \frac{3\pi }{2} < \alpha < 2\pi$

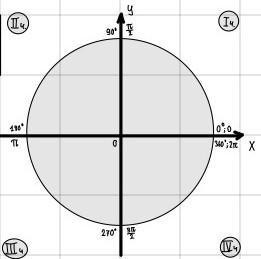
→ Для решения данной задачи, мы будем пользоваться тригонометрической единичной окружностью (см. вложение).

→ Для начала нам нужно определить четверть, в которой находится угол α.

Так как он находится между точками $\frac{3\pi }{2}$ и $2\pi$, мы можем сделать вывод, что угол α находится в IV координатной четверти. Отсюда следует, что:

$sin\alpha < 0;\\cos\alpha > 0;\\tg\alpha < 0;\\ctg\alpha < 0.$

→ Далее же приступим к самим вычислениям.

На данный момент нам известно лишь то, что $sin\alpha =-\frac{4}{5}$. Следовательно, зная синус, мы можем найти и косинус, воспользуясь основным тригонометрическим тождеством:

$sin^{2}\alpha +cos^{2} \alpha =1;$

Отсюда следует, что:

$cos^{2} \alpha = 1 - sin^{2} \alpha ;$

Значит:

$cos^{2} \alpha =1-(-\frac{4}{5} )^{2} ;\\cos^{2} \alpha =1-\frac{16}{25} ;\\cos^{2} \alpha =\frac{25}{25} -\frac{16}{25} ;\\cos^{2}\alpha =\frac{9}{25} ;\\cos\alpha =\sqrt{\frac{9}{25} } ;\\cos\alpha =\frac{3}{5} .$

__________
Удачи Вам! :)