Question

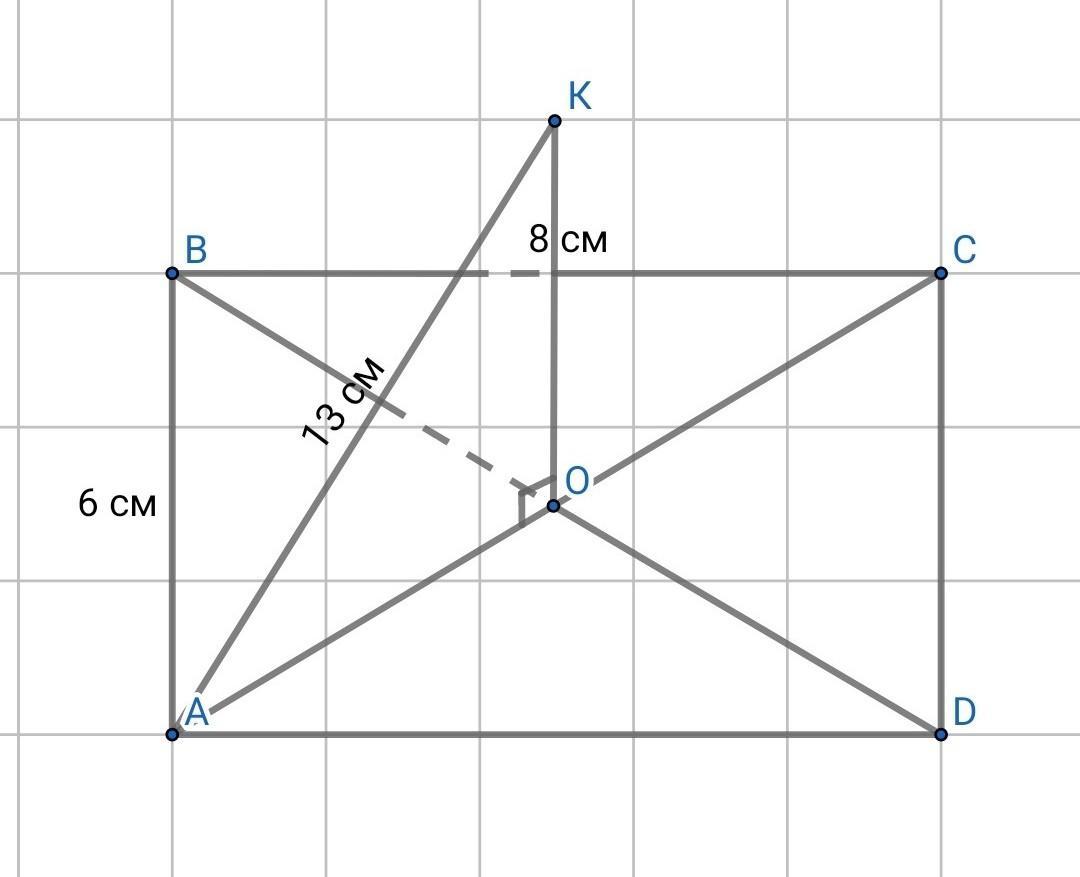
У прямокутнику ABCD зі сторонами AB=6 см, ВС= 8 см діагоналі перетинаються в точці О. ОК - перпендикуляр до площини прямокутника ABCD. Знайти відстань від точки К до площини прямокутника, якщо АК = 13 см.

Answer 1

Ответ:

Расстояние от точки К до плоскости прямоугольника равно 12(см)

Объяснение:

Дано:

ABCD - прямоугольник , АВ = 6(см) , ВС = 8(см) , О - точка пересечения диагоналей , ОК⊥(АВСD) , AK = 13(см)

Найти:

d(K;(ABCD))

Решение:

Расстояние от точки до плоскости — равно длине перпендикуляра, опущенного из точки на плоскость , значит , нам нужно найти длину ОК.

Найдем диагональ АС по т.Пифагора:

АС = √(АВ²+ВС²) = √(6²+8²) = √100 = 10(см)

Диагонали прямоугольника точкой пересечения делятся пополам .

⇒АО = 1/2АС = 5(см)

Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.

⇒△АКО - прямоугольный

По т.Пифагора найдем ОК:

ОК = √(АК²-АО²) = √(13²-5²) = √144 = 12(см)

Таким образом , d(K;(ABCD)) = 12(см)

#SPJ1