Question

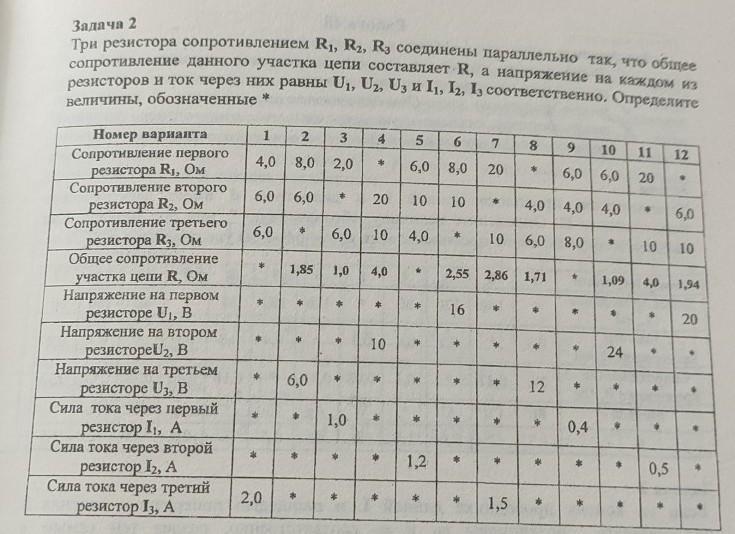
Задача 2 Три резистора сопротивлением R1, R2, R3 соединены параллельно так, что общее сопротивление данного участка цепи составляет R, а напряжение на каждом из резисторов и ток через них равны U1. Uz. Uz и I1, Iz, Iz cоответственно. Определите * величины, обозначенные Номер варианта Сопротивление первого резистора R1, Ом Сопротивление второго резистора R2, Ом Сопротивление третьего резистора R3, Ом Общее сопротивление участка цепи R, Ом Напряжение на первом резисторе U, В Напряжение на втором резистореU2, в Напряжение на третьем резисторе U3, В Сила тока через первый резистор I1, А Сила тока через второй резистор 12, А Сила тока через третий резистор 13, А 1 2 3 4,0 8,0 2,0 6,0 6,0 6,0 В ж sli К 1,85 1,0 4,0 К 2,0 4 * * 6,0 Х * * К * 4 5 6,0 10 4,0 1,0 * * 20 10 10 * 10 * X 6 6,0 8,0 * * X * * * * 1,2 * मैं 16 * * * * 7 2,55 2,86 1,71 + * 20 * 10 6,0 8,0 * * 8 9 * 10 6,0 6,0 4,0 4,0 4,0 1,5 про * + $ 12 * * В зре ⇓ * 3 * * 0,4 * * 11 20 * 1,09 4,0 1,94 24 o # И 10 10 12 1 4 4 0,5 W 6,0 + + 20 * * *
4 вар плизззз​

Answer 1

Ответ:

Используем формулу для расчета общего сопротивления параллельно соединенных резисторов:

1/R = 1/R1 + 1/R2 + 1/R3

Для первого варианта:

1/R = 1/4 + 1/8 + 1/2 = 0.875

R = 1/0.875 = 1.1429 Ом

U1 = U2 = U3 = U = 6 В

I1 = U1/R1 = 6/4 = 1.5 А

I2 = U2/R2 = 6/8 = 0.75 А

I3 = U3/R3 = 6/2 = 3 А

Для второго варианта:

1/R = 1/2 + 1/4 + 1/X

R = 1/((1/2) + (1/4) + (1/X))

Учитывая, что общее сопротивление участка цепи R = 6 Ом, получим:

1/6 = 1/2 + 1/4 + 1/X

1/X = 1/6 - 1/2 - 1/4 = -1/4

X = -4 Ом (невозможное значение сопротивления)

Для третьего варианта:

1/R = 1/6 + 1/6 + 1/4

R = 1/((1/6) + (1/6) + (1/4)) = 1.7143 Ом

U1 = U2 = U3 = U = 10 В

I1 = U1/R1 = 10/6 = 1.6667 А

I2 = U2/R2 = 10/6 = 1.6667 А

I3 = U3/R3 = 10/4 = 2.5 А

Для четвертого варианта:

1/R = 1/10 + 1/X + 1/20

R = 1/((1/10) + (1/X) + (1/20))

Учитывая, что общее сопротивление участка цепи R = 16 Ом, получим:

1/16 = 1/10 + 1/X + 1/20

1/X = 1/16 - 1/10 - 1/20 = -1/40

X = -40 Ом (невозможное значение сопротивления)

Для пятого варианта:

1/R = 1/6 + 1/6 + 1/X

R = 1/((1/6) + (1/6) + (1/X))

Учитывая, что общее сопротивление участка цепи R = 20 Ом, получим:

1/20 = 1/6 + 1/6 + 1/X

1/X = 1/20 - 1/6 - 1/6 = -1/4

X = -4 Ом (невозможное значение сопротивления)

Для шестого варианта:

1/R = 1

Объяснение: