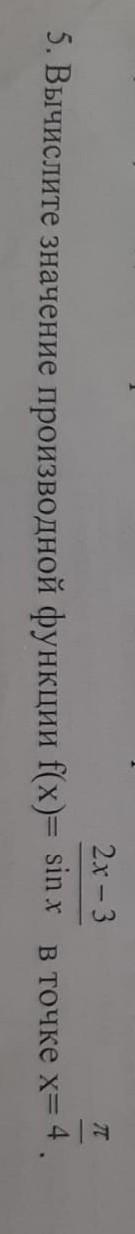Ответы
Ответ дал:
0
Ответ:
Для нахождения значения производной функции в точке x = π/4, нам сначала нужно вычислить саму производную этой функции.
Используя правило дифференцирования частного, мы можем записать:
f'(x) = [(2x - 3)cos(x) - (2)(sin(x))] / sin^2(x)
Теперь мы можем вычислить значение производной в точке x = π/4, подставив x = π/4 в выражение для f'(x):
f'(π/4) = [(2(π/4) - 3)cos(π/4) - (2)(sin(π/4))] / sin^2(π/4)
= [(π/2 - 3)√2/2 - 2(1/√2)] / (1/2)
= [(π - 6)√2 - 4√2] / (1/2)
= 2(π - 5)√2
Таким образом, значение производной функции f(x) в точке x = π/4 равно 2(π - 5)√2.
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад
8 лет назад