Ответы
Ответ дал:
1
Ответ:
Доказано: АВ + СD = BC + AD
Объяснение:
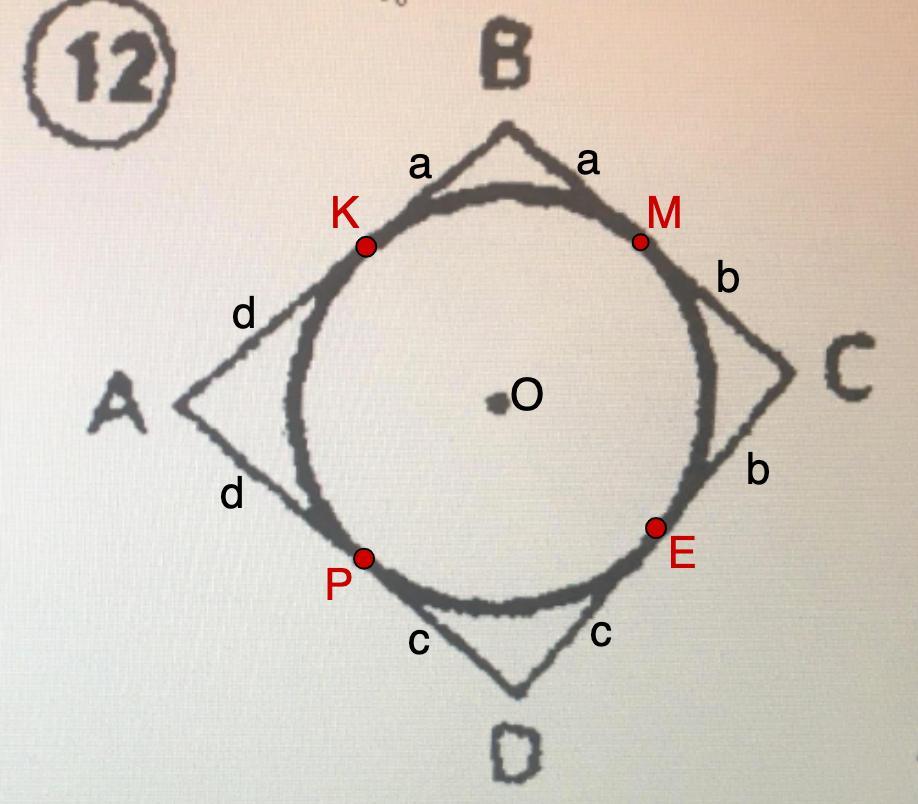
Выполнить задание по рисунку.
Дано: Окр.О;
АВСD - описанный четырехугольник;
Доказать: АВ + СD = BC + AD
Доказательство:
Так как АВСD - описанный четырехугольник около окружности, то
АВ; СD; BC; AD - касательные.
Обозначим точки касания К, М, Е, Р.
- Отрезки касательных к окружности, проведённые из одной точки, равны.
Пусть ВК = ВМ = a;
CM = CE = b;
DE = DP = c;
AK = AP = d.
Тогда
АВ + СD = d + a + b + c
BC + AD = a + b + d + c
⇒ АВ + СD = BC + AD
Если в четырехугольник вписана окружность, то суммы противоположных сторон равны.
#SPJ1
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад
