Ответы
Ответ:
кут В = 90° - 30° = 60°
кут АВК = куту КВС = 60° : 2 = 30° — бо ВК є бісектрисою
СК = 1/2 ВК — за властивістю прямокутного трикутника з кутом 30°
СК = 5 см
За теоремою Піфагора:
СВ² = ВК² - СК²
СВ² = 100 - 25 = 75
СВ = √75 = 5√3 см
АВ = 2 · 5√3 = 10√3 см — за властивістю прямокутного трикутника з кутом 30°
За теоремою Піфагора:
АС² = АВ² - СВ²
АС² = (10√3)² - (5√3)² = 300 - 75 = 225 см
АС = √225 = 15 см
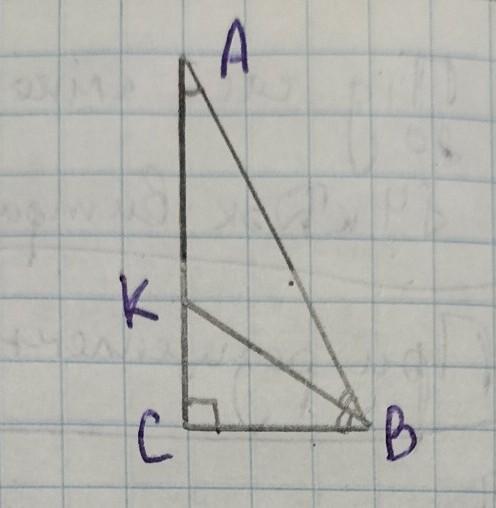
Ответ:
АС = 15см
Объяснение:
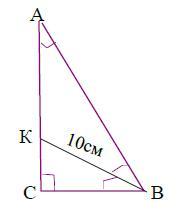
Дано:
ΔАВС
∠С = 90°
∠А =30°
ВК - биссектриса
ВК = 10см
--------------------
АС = ? см
1) Сумма углов в Δ-ке = 180°. Т.к. ΔАВС - прямоугольный (∠С = 90° по условию) и ∠А = 30°, то
∠ В = 90° - 30° = 60°
Т.к. ВК - биссектриса угла В, то
∠АВК = ∠СВК = 60°/2 = 30°
2) Рассмотрим ΔАКВ.
∠А = 30° (по условию) и ∠АВК = 30°, значит,
ΔАКВ - равнобедренный и АК = ВК = 10 (см)
3) Рассмотрим ΔКСВ..
∠С =90°, ∠СВК = 30°.
В прямоугольном Δ-ке против угла в 30° лежит катет, равный половине гипотенузы, т.е.
КС = ¹/₂ КВ = 10/2 = 5(см)
4) АС = АК + КС = 10 +5 = 15(см)