Question

розвязати рівняння розклавши його ліву частину на множники x^2-10x+9=0

Answer 1

Ответ:

вот

Пошаговое объяснение:

Answer 2

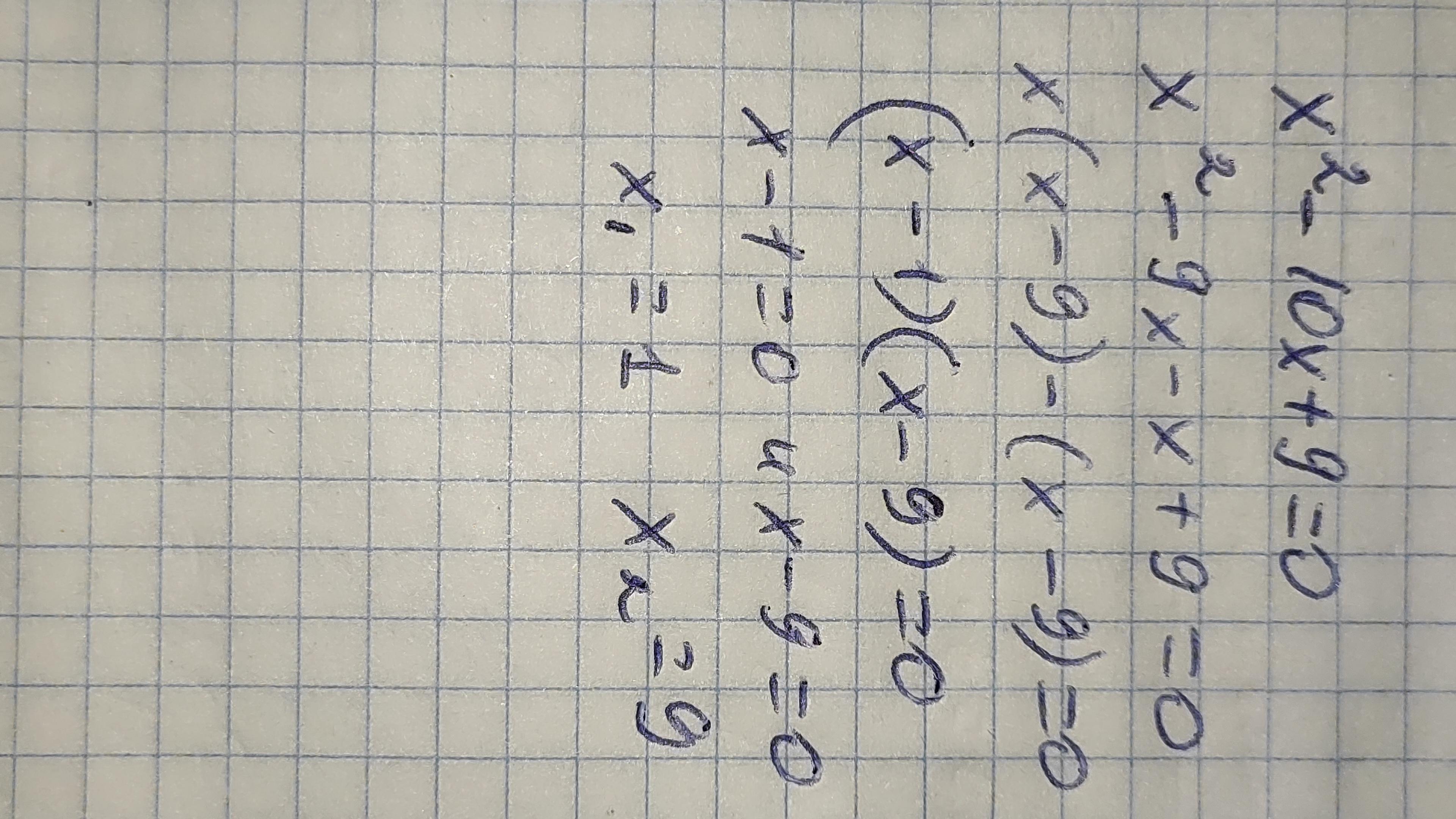
Ответ: Для розв'язання цього рівняння ми можемо використати метод розкладання лівої частини на множники.

x^2-10x+9=0

Спочатку ми знаходимо корені квадратного рівняння x^2-10x+9=0, розв'язавши його за допомогою формули коренів:

x = (10 ± √(10^2 - 419)) / 2*1

x = (10 ± √(100 - 36)) / 2

x = (10 ± √64) / 2

x1 = 9

x2 = 1

Отже, ми знайшли, що рівняння x^2-10x+9=0 має два корені: x1 = 9 і x2 = 1.

Тепер ми можемо розкласти ліву частину вихідного рівняння на множники, використовуючи ці корені:

x^3 - 9x^2 - x + 9 = (x - 9) * (x^2 - x - 1)

Отже, рівняння має два розв'язки:

x - 9 = 0, що дає x = 9;

x^2 - x - 1 = 0, що можна розв'язати, використовуючи формулу коренів для квадратних рівнянь:

x = (1 ± √(1 + 4)) / 2

x1 = (1 + √5) / 2

x2 = (1 - √5) / 2

Отже, рівняння має три розв'язки: x = 9, x = (1 + √5) / 2 і x = (1 - √5) / 2.

Пошаговое объяснение: