Question

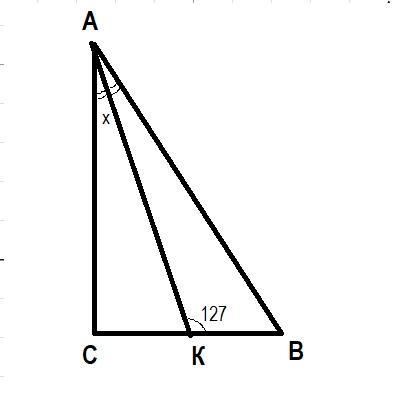
Дано трикутник АBC |_С=90 |_AKB=127,AK-бісекртиса чому дорівнює В?​

Answer 1

Ответ: 16°

Решение:

1) Пусть ∠САК = х. Тогда ∠КАВ = х и ∠А = 2х так как АК - биссектриса.

2) Δ АВС, то теореме о сумме углов треугольника

∠А+∠В+∠С = 180°

2х + ∠В +90 = 180

∠В = 180 - 90 - 2х = 90 - 2х

3) Δ АКВ, то теореме о сумме углов треугольника

∠КАВ + ∠В + ∠АКВ = 180

х + ∠В +127 = 180

х + 90 - 2х + 127 = 180

х = 37

∠В = 90 - 2х = 90 - 2*37 = 16

Ответ:  16°