Question

Допоможіть будь ласка даю 50 балів!!!​

Answer 1

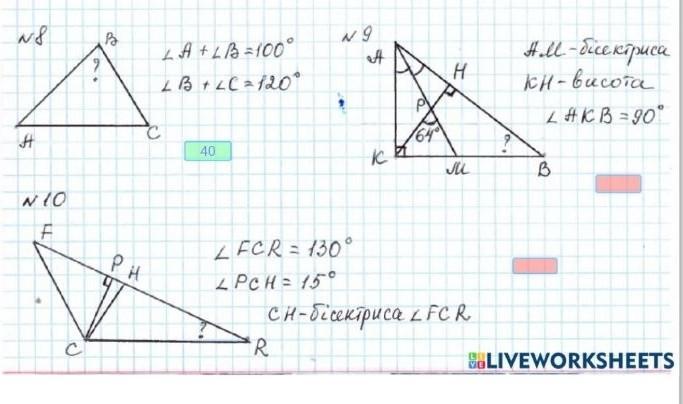
ЗАДАНИЕ 8

1      Сумма углов в треугольнике равна 180°

      ∠А + ∠B + ∠С = 180°   подставим ∠А + ∠B = 100°

      100° + ∠С = 180    

      ∠С = 180° - 100° = 80°    

2     Зная ∠С  найдем  ∠B

       ∠B + ∠С = 120°    подставим ∠С = 80°

       ∠B + 80° = 120°

      ∠B = 120° - 80° = 40°

      ОТВЕТ: ∠B = 40°

ЗАДАНИЕ 9

1      ∠KPM =  ∠APH = 64° ( вертикальные углы равны)

2     Рассмотрим △APH:  ∠P = 64°

                                         ∠H = 90°  (т.к. КН - высота)

                                         ∠А = 180°-∠P-∠А = 180°-64°-90° = 26°

3    ∠KАM =  ∠MAB = 26° (т.к. AM - медиана)

     ∠KАB =  ∠KАM + ∠MAB = 26° + 26° = 52°  (∠А в △KAB)

4   Рассмотрим △KAB:   ∠K = 90°

                                        ∠A = 52°

                                        ∠B = 180°-∠K-∠А = 180°-90°-52° = 38°

      ОТВЕТ: ∠B = 38°

ЗАДАНИЕ 10

1     ∠FCH = ∠HСR = ∠FCR/2 = 130/2 = 65°  (т.к. СH бисектриса)

2    ∠РНС = 180° - ∠СPH - ∠РСH = 180° - 90° - 15° = 75°

3    ∠РНС и ∠СHR смежные

     ∠СHR = 180° - ∠РНС = 180°- 75° = 105°

4    рассмотрим △СHR:  ∠HСR = 65°

                                         ∠СHR  = 105°

                                         ∠СRH = 180°- ∠HСR- ∠СHR =180°- 65°- 105° = 10°

ОТВЕТ: ∠СRH = 10°