помогите пожалуйста. дам 100б.
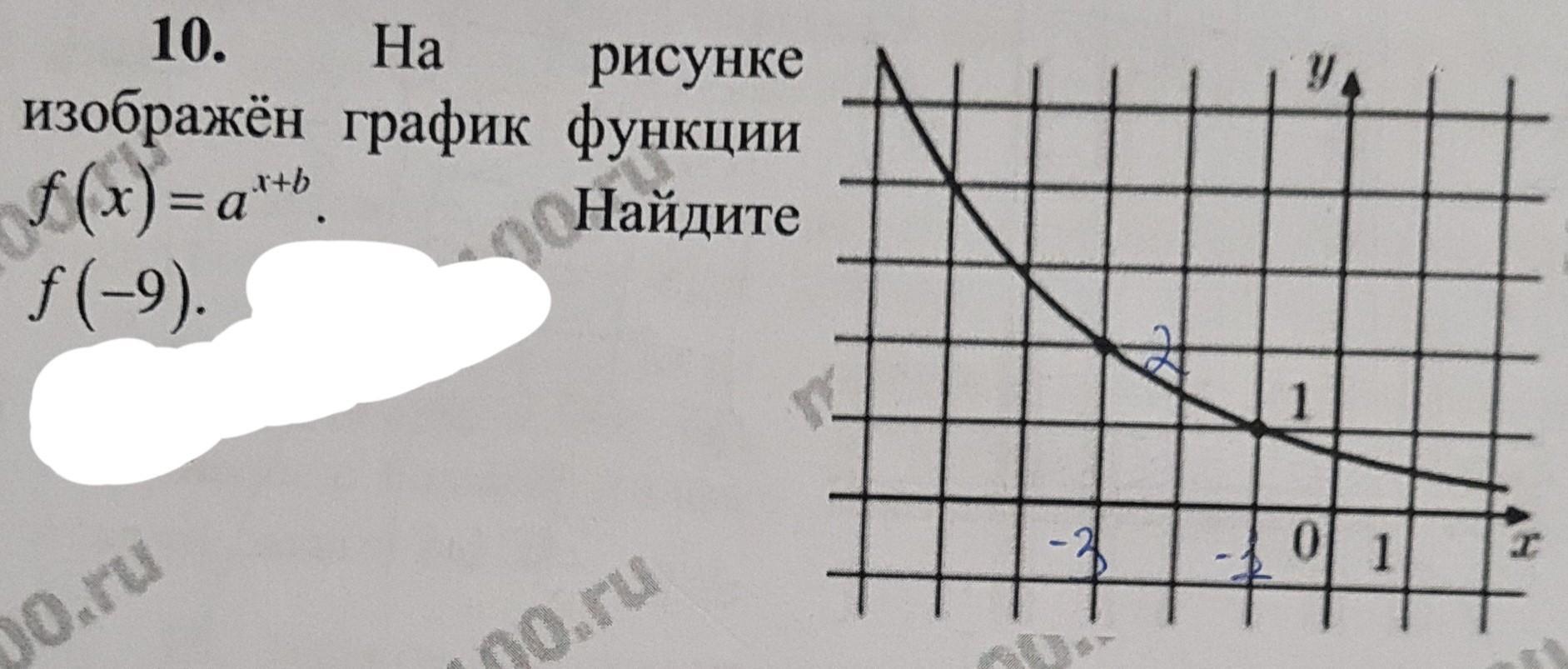
на рисунке изображён график функции f(x)=a^(x+b). найдите f(-9)
Приложения:
Ответы
Ответ дал:
1
График смещён влево по оси х на 1, значит b = 1
Рассмотрим точку ( - 3 ; 2 ):
Второй корень не подходит, т.к. 0<а<1
Ответ: 16
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад