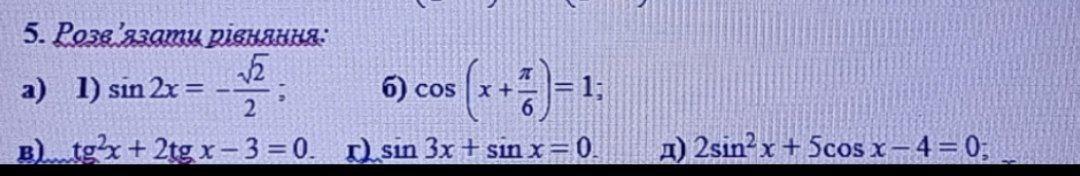Ответы
а) sin2x=-((√2)/2)
sin2x=-sin(π/4)
2x=π/4+πk или 2x=3π/4+πk (где k∈Z)
x=π/8+πk/2 или x=3π/8+πk/2 (где k∈Z)
б)cos(x+(π/6))=1
x+(π/6)=2πk или x+(π/6)=2πk+2π (где k∈Z)
x=2πk-(π/6) или x=2πk+(11π/6) (где k∈Z)
в)Проведём замену tg x = t.
Тогда, tg^2x = t^2.
Исходное уравнение примет вид t^2 + 2t - 3 = 0.
Решим это уравнение с помощью квадратного корня:
D = b^2 - 4ac = 2^2 - 4*1*(-3) = 16.
t1 = (-b + sqrt(D)) / 2a = ( -2 + 4) / 2 = 1.
t2 = (-b - sqrt(D)) / 2a = (-2 - 4) / 2 = -3.
Таким образом, получаем:
tg x = t1 = 1.
tg x = t2 = -3.
Для первого значения получаем два решения:
tgx = 1 => x = arctg(1) + kπ = π/4 + kπ.
г)sin(3x) + sin(x) = 0
3sin(x) - 4sin^3(x) + sin(x) = 0 # применяем формулу для sin(3x)
sin(x)(3 - 4sin^2(x) + 1) = 0
sin(x)(4sin^2(x) - 3) = 0
Таким образом, мы получили уравнение, которое можно решить следующим образом:
sin(x) = 0 => x = kπ, где k - целое число.
4sin^2(x) - 3 = 0 => sin^2(x) = 3/4 => sin(x) = ±sqrt(3)/2.
Заметим, что тут два решения, поскольку мы имеем дело со знаком ±. Они соответствуют углам π/3 и 2π/3:
x = π/3 + k2π, x = 2π/3 + k2π, где k - целое число.
д)Перепишем уравнение, заменив sin^2(x) на 1 - cos^2(x):
2(1 - cos^2(x)) + 5cos(x) - 4 = 0
2cos^2(x) - 5cos(x) + 2 = 0
Можно решить это квадратное уравнение относительно переменной cos x. Найдём корни этого уравнения с помощью формулы для квадратного корня:
D = b^2 - 4ac = 5^2 - 4*2*2 = 9
cos(x) = (5 + sqrt(D)) / 4 или cos(x) = (5 - sqrt(D)) / 4
cos(x) = (5 + 3) / 4 = 2 или cos(x) = (5 - 3) / 4 = 1/2
Таким образом, получаем два значения для cos(x):
cos(x) = 2 => нет решений, поскольку косинус угла не может быть больше 1 или меньше -1.
cos(x) = 1/2 => x = π/3 + 2πk или x = 5π/3 + 2πk, где k - любое целое число.