Question

Терміново!!!!!!!!!!!​

Answer 1

Відповідь:

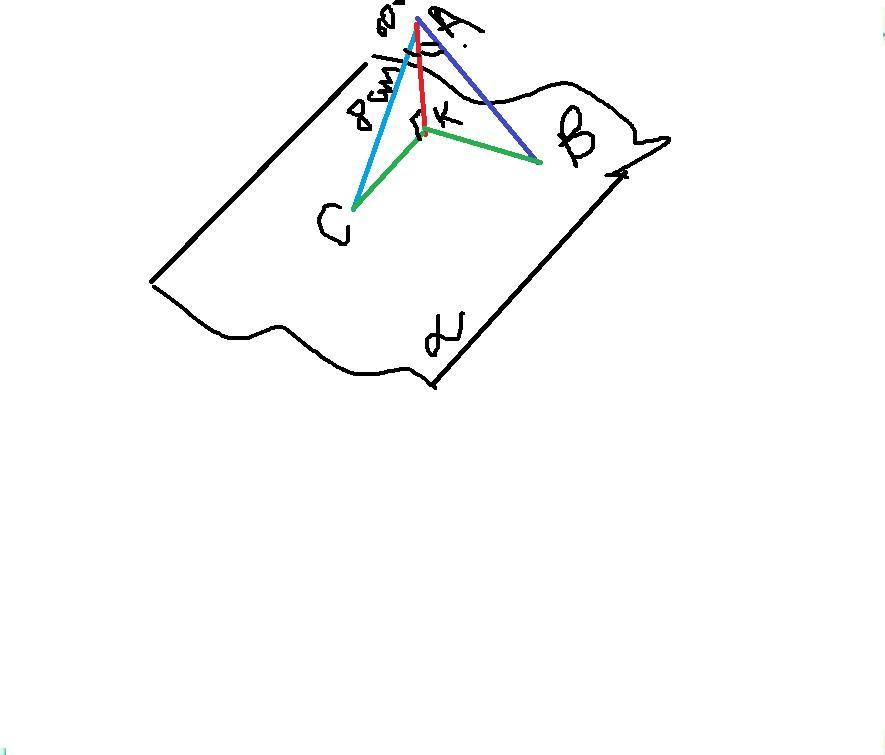
ВК= 4 см
СК=4√2 см

Пояснення:

Дано: α- площина , АК⊥α, АС= 8 см, ∠САК=60°, ∠ВАК=45°

Знайти: СК, ВК-?
Рішення:
Розглянемо ΔСАК, ∠К =90°, як кут між перпендикуляром та площиною, ∠САК=60°, CA=8 cм.

За теоремою про суму гострих кутів прямокутного  трикутника

∠С+∠САК=90° →∠С=90°- ∠САК=90°-60°=30°.
Проти кута в 30° лежить катет, що дрівнює половині гіпотенузи. Отже АК=0,5АС=05*8 см=4см.
За теоремою Піфагора АС²=АК²+СК²→ СК²=АС²-АК² →

$CK=\sqrt{8^2-4^2}=\sqrt{64-16}=\sqrt{48}=\sqrt{16*3}=4\sqrt{3}$ (см)

ΔСАК, ∠К =90°, як кут між перпендикуляром та площиною, ∠ВАК=45°, AК=4 cм.

За теоремою про суму гострих кутів прямокутного  трикутника

∠В+∠ВАК=90° →∠В=90°- ∠ВАК=90°-45°=45°.
ΔСАК- рівнобедрений, за визначенням (∠В=ВАК), отже АК=ВК, як бічні сторони. ВК= 4 см