Question

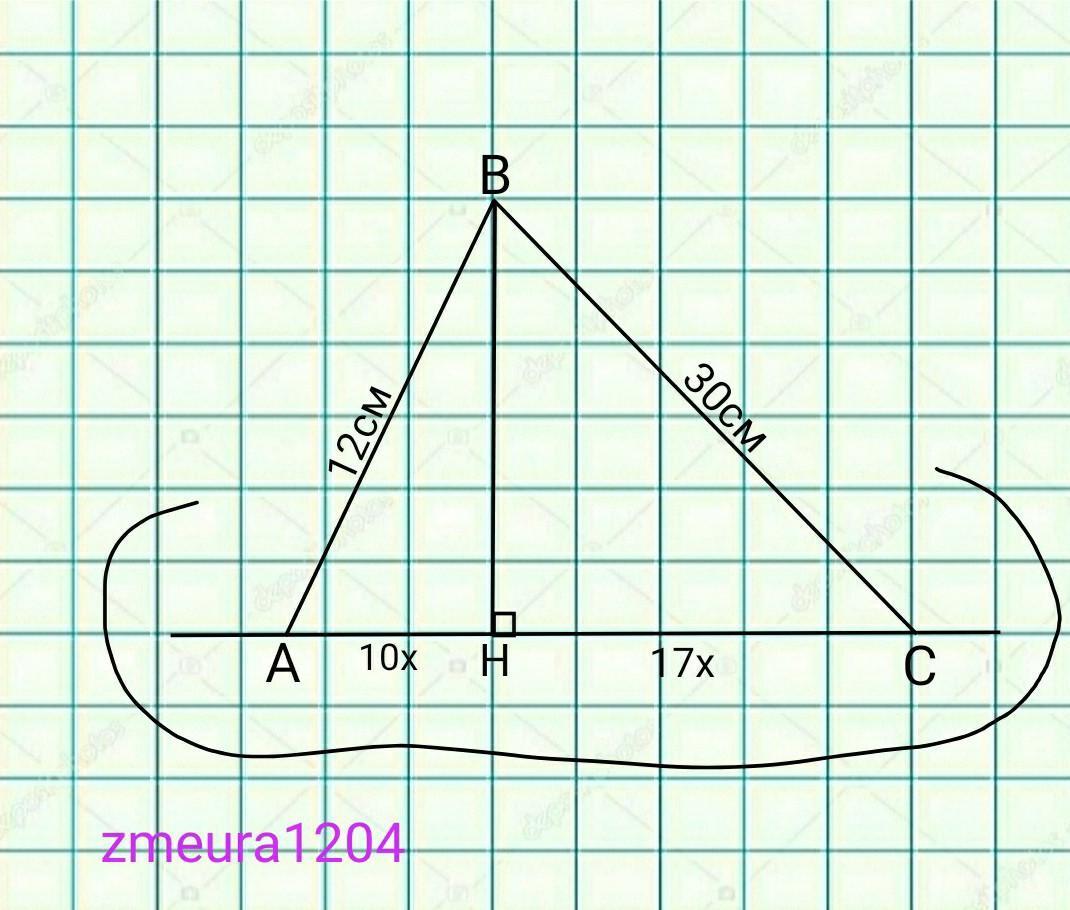
3 точки В до площини у проведено перпендикуляр ВО і похилі ВА і ВС. Відомо, що ВА = 12см, ВС=30см, проекції похилих на площину у відносяться як 10:17. Знайдіть довжину проекції похилої ВА на площину у.​

Answer 1

Ответ:

Проекція похилої АВ на площину у дорівнює 20см

Объяснение:

АН=10х; проекція похилої АВ

НС=17х; проекція похилої ВС.

∆АВН- прямокутний трикутник.

За теоремою Піфагора:

ВН²=АВ²-АН²

ВН²=12²-(10х)²

ВН=144-100х²

∆ВСН- прямокутний трикутник.

За теоремою Піфагора:

ВН²=ВС²-НС²

ВН²=30²-(17х)²

ВН²=900-289х²

ВН²=ВН²

Складаємо рівняння:

144-100х²=900-289х²

289х²-100х²=900-144

189х²=756

х²=756/189

х²=4

х=√4

х=2

АН=10х=10*2=20 см