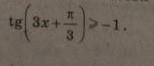Ответы
Ответ дал:
0
Віднімаємо π/3 від обох боків нерівності:
tg(3x+π/3) - π/3 ≥ -1 - π/3
Спрощуємо праву частину:
tg(3x+π/3) - π/3 ≥ -4π/3
Використовуємо тригонометричну тотожність:
tg(a - π/2) = -ctg(a)
Отже, маємо:
ctg(3x) ≥ -4π/3
Переносимо ctg(3x) на ліву сторону і домножаємо на -1:
-ctg(3x) ≤ 4π/3
Використовуємо тригонометричну тотожність:
-ctg(a) = tg(a - π)
Отже, маємо:
tg(3x - π) ≤ 4π/3
Знаходимо значення аргументу, використовуючи табличні значення тангенса:
tg(-π/3) = -√3
Розв'язуємо нерівність, виключаючи періодичні розв'язки:
3x - π ≤ arctg(-√3) + kπ, де k - ціле число
3x ≤ -0.928 + π/3 + kπ
x ≤ (-0.928 + π/3 + kπ) / 3, де k - ціле число
Таким чином, розв'язком нерівності є:
x ≤ (-0.928 + π/3) / 3 ≈ -0.472, або x ≤ (2π/3 - 0.928 + kπ) / 3, де k - ціле число.
vasya6383:
А шо таке arctg?
Вас заинтересует
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад