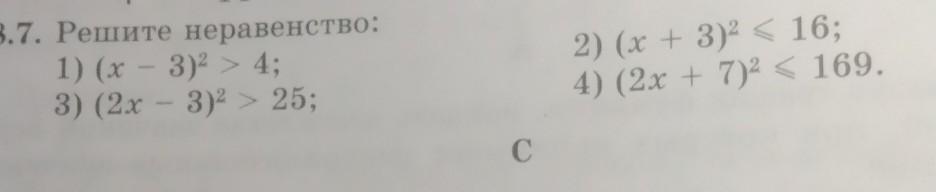Question

18.7. Решите неравенство: ​

Answer 1

Ответ и Объяснение:

Нужно знать: 1) Формулу сокращённого умножения:

a²–b² = (a–b)·(a+b).

2) Метод интервалов: Если квадратный трёхчлен разложен на множители (x–x₁)·(x–x₂) и x₁ < x₂, то

а) (x–x₁)·(x–x₂) < 0 на множестве (x₁; x₂);

б) (x–x₁)·(x–x₂) > 0 на множестве (–∞; x₁) ∪ (x₂; +∞)

Решение. Для решения неравенств сначала разложим на множители, а потом применим метод интервалов.

1) (x–3)² > 4

(x–3)²–2² > 0

(x–3–2)·(x–3+2) > 0

(x–5)·(x–1) > 0

x₁ = 1 < x₂ = 5: x ∈ (–∞; 1) ∪ (5; +∞).

2) (x+3)² ≤ 16

(x+3)²–4² ≤ 0

(x+3–4)·(x+3+4) ≤ 0

(x–1)·(x–(–7)) ≤ 0

x₁ = –7 < x₂ = 1: x ∈ [–7; 1].

3) (2·x–3)² > 25

(2·x–3)²–5² > 0

(2·x–3–5)·(2·x–3+5) > 0

(2·x–8)·(2·x+2) > 0

4·(x–4)·(x–(–1)) > 0

(x–4)·(x–(–1)) > 0

x₁ = –1 < x₂ = 4: x ∈ (–∞; –1) ∪ (4; +∞).

4) (2·x+7)² ≤ 169

(2·x+7)²–13² ≤ 0

(2·x+7–13)·(2·x+7+13) ≤ 0

(2·x–6)·(2·x+20) ≤ 0

4·(x–3)·(x+10) ≤ 0

(x–3)·(x–(–10)) ≤ 0

x₁ = –10 < x₂ = 3: x ∈ [–10; 3].

#SPJ1