Question

Найди длину высоты равностороннего треугольника,если его сторона равна 3в корне

Answer 1

Известно, что для равностороннего треугольника сторона равна 3 в корне, а высота, как биссектриса, делит эту сторону на две части, пропорциональные длинам смежных сторон треугольника. Таким образом, длина половины стороны равна:

(1/2) * 3 в корне = (3/2) в корне

Теперь, с помощью теоремы Пифагора, мы можем найти длину высоты, которая является гипотенузой прямоугольного треугольника, образованного половиной стороны и искомой высотой:

h^2 = (3/2)^2 - (3/6)^2 = 9/4 - 3/16 = 33/16

h = sqrt(33)/4 в корне

Таким образом, длина высоты равностороннего треугольника равна sqrt(33)/4 в корне.

Answer 2

Ответ:

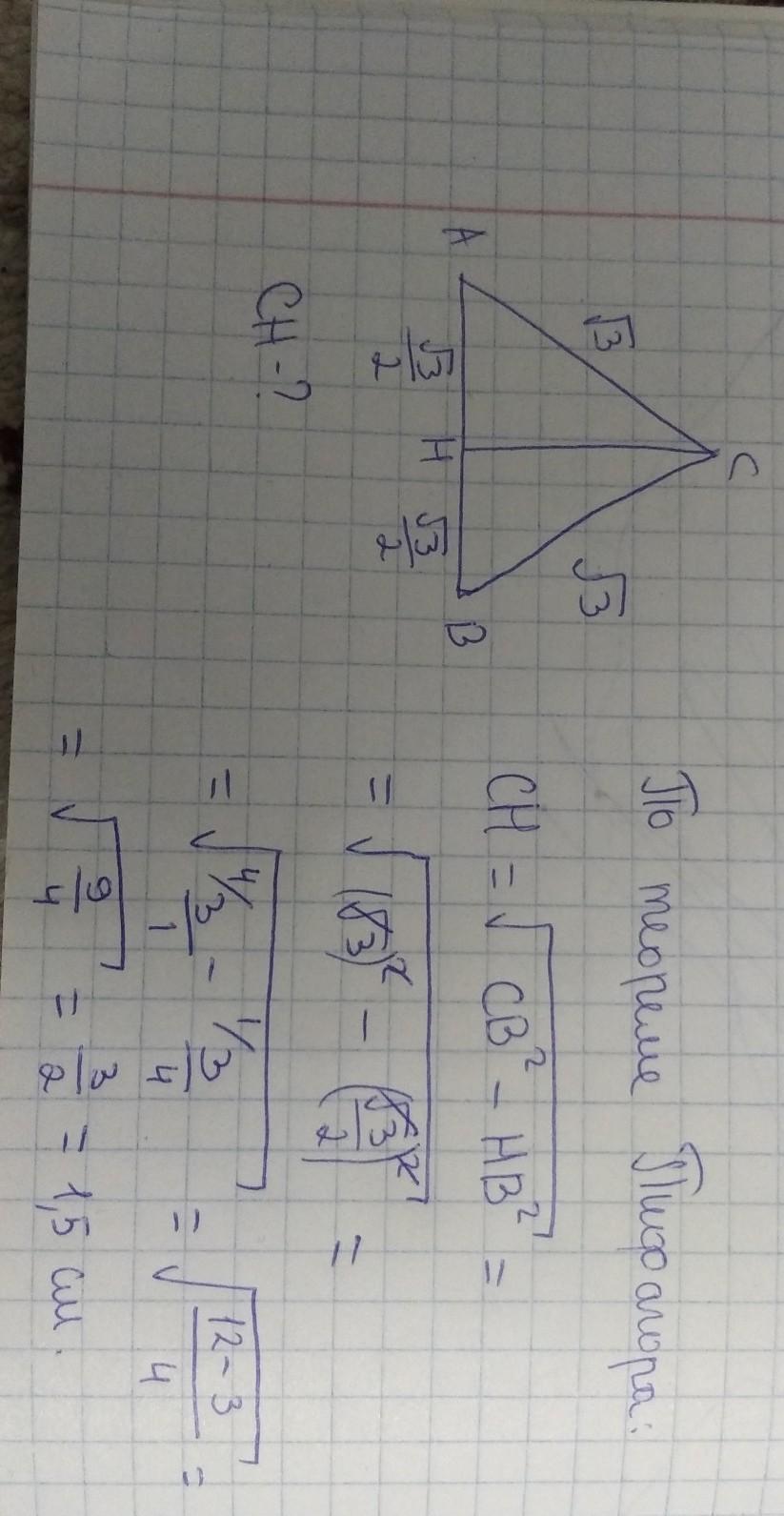
Решаем по теореме Пифагора