Question

фото, помогите пожалуйста

Answer 1

Ответ:

Відстань між основами медіани і висоти дорівнює 6 см.

Объяснение:

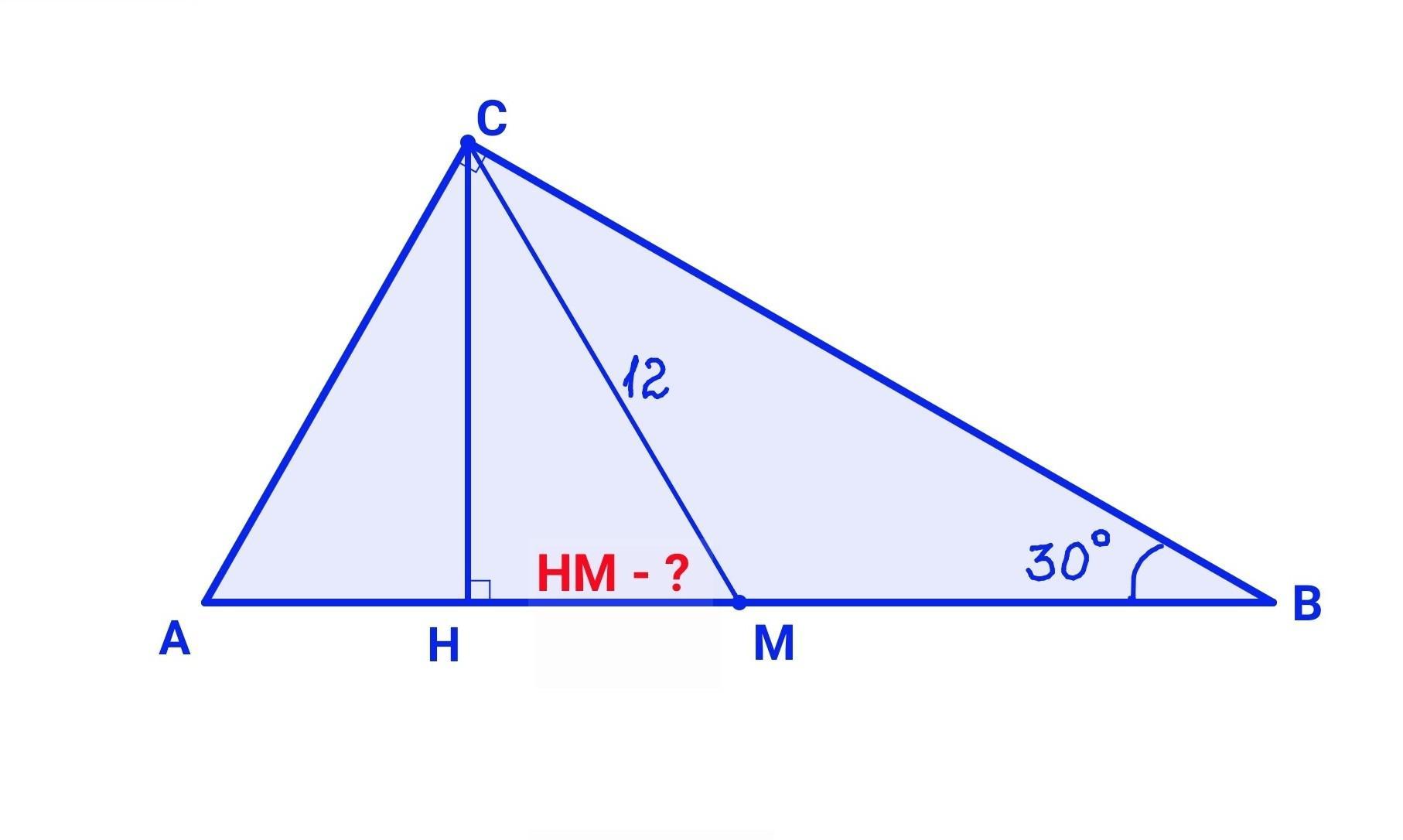
Один із кутів прямокутного трикутника дорівнює 30°. Знайдіть відстань між основами медіани і висоти, проведеними з вершини прямого кута, якщо медіана дорівнює 12 см.

• Медіана прямокутного трикутника, проведена до гіпотенузи, дорівнює її половині.
• Катет прямокутного трикутника, що лежить проти кута 30°, дорівнює половині гіпотенузи.
• Висота рівнобедреного трикутника, проведена до основи, є його медіаною і бісектрисою.

Нехай АВС - даний прямокутний трикутник. ∠С=90°, ∠В=30°, СН - висота, СН⟂АВ, СМ - медіана, АМ=МВ.

Знайдемо НМ.

1) СМ - медіана прямокутного трикутника АВС, проведена до гіпотенузи. Тому:

СМ=½•АВ.

Оскільки АМ=МВ=½•АВ, то АМ=МВ=СМ=12 (см),

АВ=2•СМ=2•12=24(см)

2) В трикутнику АВС:

Катет АС лежить проти кута ∠В=30°, тому:

АС=½•АВ=½•24=12(см)

АС=АМ, тому △АСМ - рівнобедрений з основою АМ.

АН - висота рівнобедреного трикутника, отже є також його медіаною:

АН=НМ=½•АМ=½•12= 6 (см)

Відповідь: 6 (см)