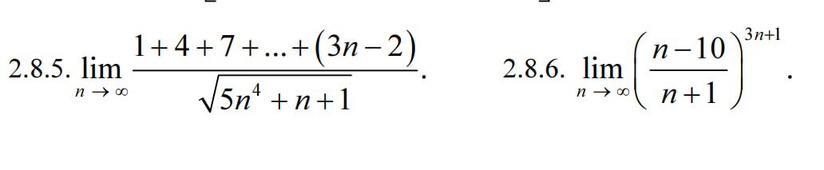Ответы
Ответ дал:
0
Ответ:
Объяснение:
2.8.5.
1+4+7+...+(3n-2) - это сумма n членов арифметической прогрессии,
где d=3 a1=1
Воспользуемся формулой для суммы n первых членов арифметической прогрессии Sn= (2a1+d(n-1))*n/2
=> Sn= (2+3(n-1))n/2= n(3n-1)/2 =(3n²-n)/2
=>
2.8.6
Воспользуемся замечательным пределом lim( 1+1/x)^x=e (x->∞)
=>
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад