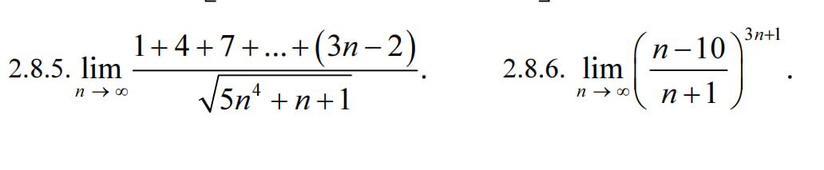Ответы
Ответ дал:
1
Ответ:
2.8.5.
В числителе записана сумма членов арифметической прогрессии с разностью d=3 и первым членом а₁=1 . Вычислим сумму n членов арифметической прогрессии по формуле
.
2.8.6.
Применим второй замечательный предел .
06avrora:
Большое Вам спасибо, хорошей ночи!
Пожалуйста
Вас заинтересует
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад