Ответы
Ответ дал:
1
Ответ:
Интегрирование по частям: .
10) Применим интегрирование по частям два раза .
Перенесём интеграл из правой части равенства в левую, получим
Приложения:
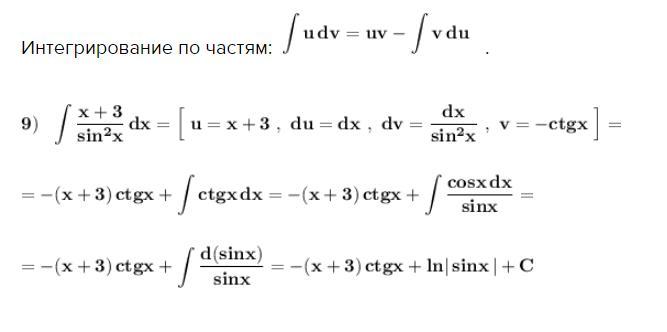

Аноним:
огромное спасибо
вы очень хорошая объясняете)
все примеры в которым я не разобрался я добавил их , потом посмотрите пожалуйста
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
8 лет назад
