Исследовать на сходимость (если можно то примените признак Лейбница)
Объясните все подробно пожалуйста)
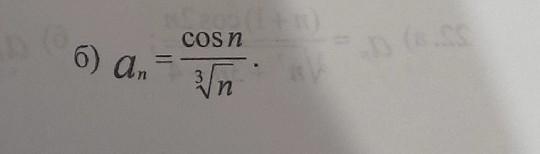
Ответы
Ответ:
Сходится.
Объяснение:
Дан ряд
Он не является знакочередующимся, поэтому признак Лейбница применить нельзя. Но есть более мощные признаки сходимости знакопеременных рядов. Мы применим признак Дирихле (признак Лейбница - это частный случай признака Дирихле).
ПРИЗНАК ДИРИХЛЕ.
Пусть нам дан ряд причем
1) частичные суммы ряда ограничены, то есть существует такое число K, что для любого натурального n выполнено
2)
3)
Тогда ряд сходится.
В нашем случае где
То, что выполнены условия 2) и 3) сомнений нет (когда дают задачу на признак Дирихле или признак Абеля, аккуратно проверять такую ерунду не заставляют). Проверим первое условие. Надо сказать, данный ряд (с возможной заменой косинуса на синус и изменения степени n в знаменателе) изучают в любом продвинутом курсе математики. Применим следующий искусственный способ (придумать его самому, без подсказки, на мой взгляд затруднительно).
Рассмотрим произведение Имеем:
Поэтому
откуда
Тем самым первое условие выполнено, а раз второе и третье условия очевидно также выполнены, сходимость исходного ряда доказана с помощью признака Дирихле.
Замечание. Поскольку в условии ничего не сказано про абсолютную и условную сходимость, считаю свое решение исчерпывающим.
Замечание. Ограниченность частичных сумм можно было бы доказать и другим способом (с использованием комплексных чисел), но я думаю, что и одного способа достаточно.