Question

очень срочно,помогите пожалуйста​

Answer 1

Ответ:
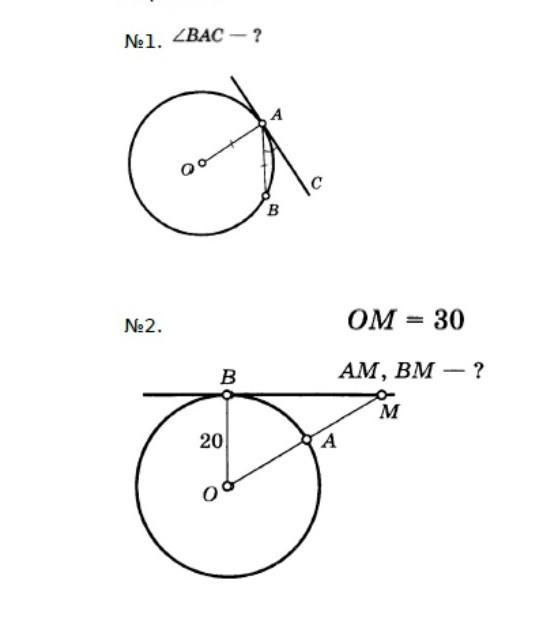
1)∠ВАС=30°

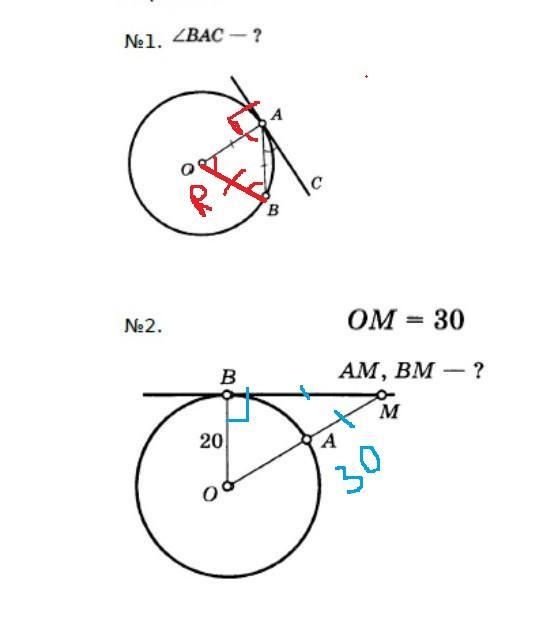
2) BM=AM=10√5
Решение:

1)Проведём ОВ
ОА=ОВ=ОС=R , как радиус окружности. Следовательно ΔАОВ- равносторонний. По свойству углов равностороннего треугольника: ∠А=∠В=∠С=60°.( ∠А+∠В+∠С=180°;∠А=180°:3=60°)
АС⊥ОА, как касательная, проведённая к радиусу→ ∠ОАС=90°
∠ВАС=∠ОАС-∠ОАВ=90°-60°=30°

2) ВМ⊥ОВ,как касательная, проведённая к радиусу.
ВМ=АМ, по свойству касательных, проведённых из одной точки
Рассмотрим ΔОВМ, ∠В=90°, ОВ=20, ОМ=30
Согласно теореме Пифагора
ОМ²=ОВ²+ВМ²; →ВМ²=ОМ²-ОВ²=30²-20²=(30-20)(30+20)=10*50=500
$BM=\sqrt{500}=\sqrt{5*100}=10\sqrt{5}$