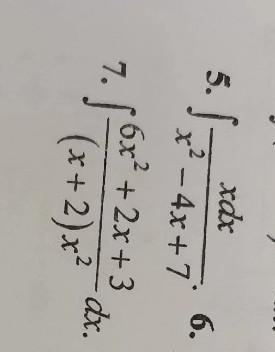Question

Помогите пожалуйста решить интеграл ​

Answer 1

Ответ:

5.     $\displaystyle \int\limits {\frac{x\;dx}{x^2-4x+7} }=\frac{1}{2}ln|x^2-4x+7|+\frac{2}{\sqrt{3} } \; arctg\frac{x-2}{\sqrt{3} } +C$

7.     $\displaystyle \int\limits {\frac{6x^2+2x+3}{(x+2)x^2} } \, dx=\frac{23}{4}ln |x+2|-\frac{3}{2x} +\frac{1}{4}ln|x|+C$

Объяснение:

Вычислить интегралы:

5.     $\displaystyle \bf \int\limits {\frac{x\;dx}{x^2-4x+7} }$

7.     $\displaystyle \bf \int\limits {\frac{6x^2+2x+3}{(x+2)x^2} } \, dx$

5. Преобразуем интеграл:

$\displaystyle \frac{1}{2} \int\limits {\frac{2x\;dx}{x^2-4x+7} }=\frac{1}{2} \int\limits {\frac{2x-4+4}{x^2-4x+7} } \, dx =\\\\\\=\frac{1}{2} \int\limits {\frac{2x-4}{x^2-4x+7} } \, dx +\frac{1}{2} \int\limits {\frac{4}{x^2-4x+7} } \, dx$

1) Первый интеграл.

Замена переменной:

$\displaystyle x^2-4x+7 = t\\\\(2x-4)dx=dt$

Получим интеграл:

$\displaystyle \frac{1}{2}\int\limits {\frac{ dt}{t} } =\frac{1}{2}ln|t|+C=$

Обратная замена:

$\displaystyle \bf =\frac{1}{2} ln|x^2-4x+7|+C$  

2) Второй интеграл.

В знаменателе выделим полный квадрат:

$\displaystyle \frac{4}{2}\int\limits {\frac{1}{x^2-4x+4+3} } \, dx =2\int\limits {\frac{d(x-2)}{(x-2)^2+3} }=$

$\boxed {\displaystyle \bf \int\limits {\frac{dx}{x^2+a^2} } =\frac{1}{a}arc tg\frac{x}{a}+C }$

$\displaystyle \bf =\frac{2}{\sqrt{3} }arctg\frac{x-2}{\sqrt{3} }+C$

В итоге получим:

$\displaystyle \bf \int\limits {\frac{x\;dx}{x^2-4x+7} }=\frac{1}{2}ln|x^2-4x+7|+\frac{2}{\sqrt{3} } \; arctg\frac{x-2}{\sqrt{3} } +C$

7.     $\displaystyle \bf \int\limits {\frac{6x^2+2x+3}{(x+2)x^2} } \, dx$

Представим подинтегральное выражение в виде суммы простейших дробей.

Множителю (х +2) соответствует простейшая дробь:

$\displaystyle \frac{A}{x+2}$

Множителю х² соответствует сумма простейших дробей:

$\displaystyle \frac{B}{x^2}+\frac{C}{x}$

Следовательно:

$\displaystyle \frac{6x^2+2x+3}{(x+2)x^2} =\frac{A}{x+2}+\frac{B}{x^2} +\frac{C}{x}$

Освободимся от знаменателя:

$\displaystyle 6x^2+2x+3=Ax^2+B(x+2)+Cx(x+2)\\\\6x^2+2x+3=Ax^2+Bx+2B+Cx^2+2Cx\\\\6x^2+2x+3=(A+C)x^2+(B+2C)x+2B$

Сравним коэффициенты при одинаковых степенях х.

Получим систему:

$\begin{equation*} \begin{cases} A+C=6 \\B+2C=2 \\2B =3 \end{cases}\end{equation*}$

$\displaystyle B=\frac{3}{2} ;\\\\\frac{3}{2} +2C=2\;\Rightarrow \;C=\frac{1}{4} \\\\A+\frac{1}{4} =6\;\Rightarrow \;A=\frac{23}{4}$

$\displaystyle \frac{6x^2+2x+3}{(x+2)x^2} =\frac{23}{4(x+2)}+\frac{3}{2x^2} +\frac{1}{4x}$

Вычислим интеграл:

$\displaystyle \int\limits {\frac{6x^2+2x+3}{(x+2)x^2} } \, dx =\frac{23}{4} \int\limits {\frac{1}{x+2} } \, d(x+2) +\frac{3}{2}\int\limits {x^{-2}} \, dx +\frac{1}{4}\int\limits {\frac{1}{x} } \, dx =\\\\\\=\frac{23}{4}ln|x+2|+\frac{3}{2}\cdot\frac{x^{-1}}{-1} +\frac{1}{4}ln|x|=\\ \\\\=\frac{23}{4}ln |x+2|-\frac{3}{2x} +\frac{1}{4}ln|x|+C$