Question

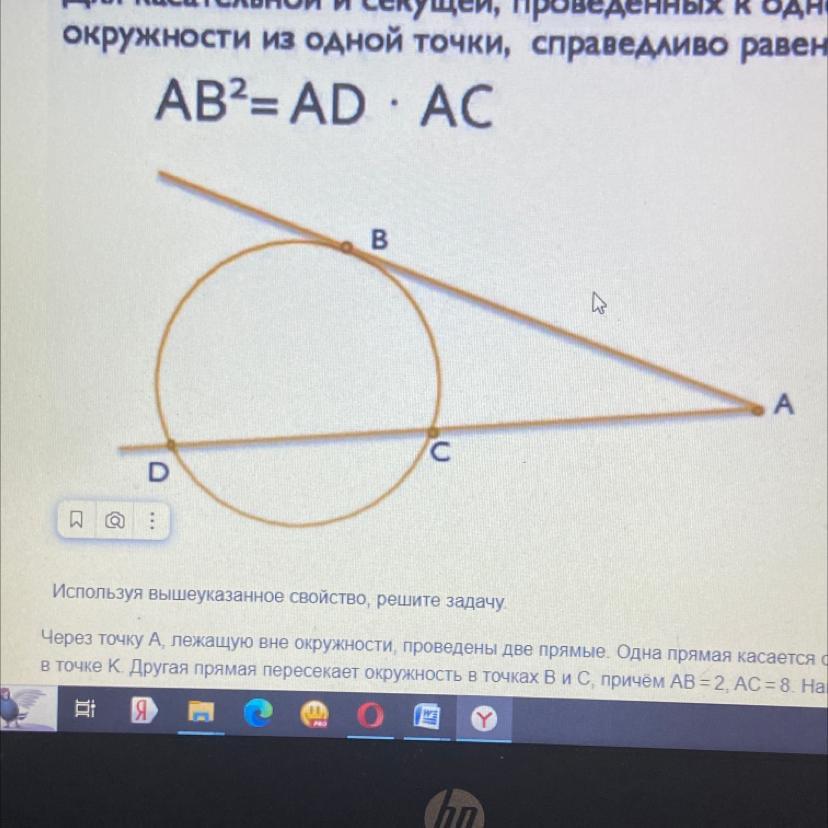
через точку А, лежащую вне окружности, проведены две прямые. одна прямая касается окружности в точке К. другая прямая пересекает окружность в точках В и С, причем АВ = 2, АС = 8. найдите АК

Answer 1

Для решения задачи воспользуемся свойством, которое гласит: если из точки, лежащей вне окружности, провести касательную к этой окружности, а затем из той же точки провести секущую, пересекающую окружность в точках В и С, то произведение отрезков АВ и АС равно квадрату длины касательной АК: AB·AC=AK².

Используем данное свойство для нахождения АК:

AB·AC=AK²,

2·8=AK²,

16=AK².

Отсюда получаем, что AK=4√2 (так как корень из 16 равен 4, а значит, корень из 16 умноженный на корень из 2 равен 4√2).

Таким образом, АК равно 4√2.