Ответы
Ответ:
1.
1.
Объяснение:
12. Радиусы окружностей оснований шарового слоя 3 м и 4 м, а радиус шара равен 5 м. Найдите объем шарового слоя (рассмотреть два случая).
Дано: Шар(О,R)
Окр.(А,R₁) и Окр.(Е,R₂) - основания шарового слоя.
R = 5м; R₁ = 3м; R₂ = 4м.
Найти: V шарового слоя.
Решение:
- Шаровым слоем называется часть шара расположенная между двумя параллельными плоскостями, пересекающими шар.
- Формула объема шарового слоя:
V = (π / 6) * h * (3R² + 3r² + h²)
где R, r — радиусы оснований, h — высота.
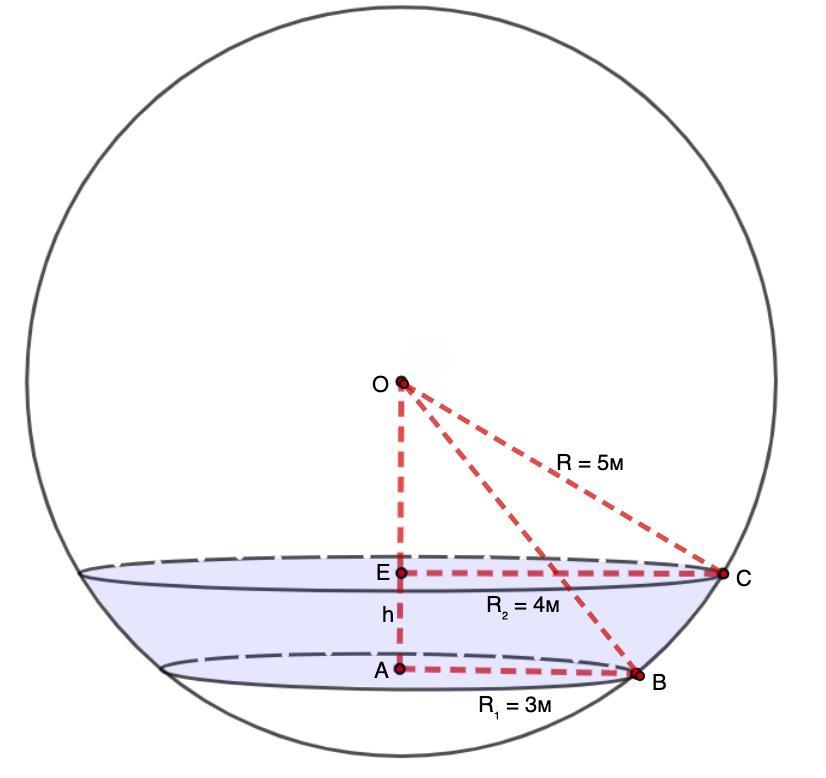
1. Основания шарового слоя лежат по одну сторону от центра шара.
- Любое сечение шара плоскостью есть круг. Перпендикуляр, опущенный из центра шара на секущую плоскость, попадает в центр этого круга.
⇒ ОЕ ⊥ ЕС; ОА ⊥АВ.
Рассмотрим ΔЕОС - прямоугольный.
По теореме Пифагора:
ОЕ² = ОС² - ЕС² = 25 - 16 = 9 ⇒ ОЕ = 3 м.
Рассмотрим ΔАОВ - прямоугольный.
По теореме Пифагора:
ОА² = ОВ² - АВ² = 25 - 9 = 16 ⇒ ОА = 4 м.
h = ЕА = ОА - ОЕ = 4 - 3 = 1 (м)
Найдем объем:
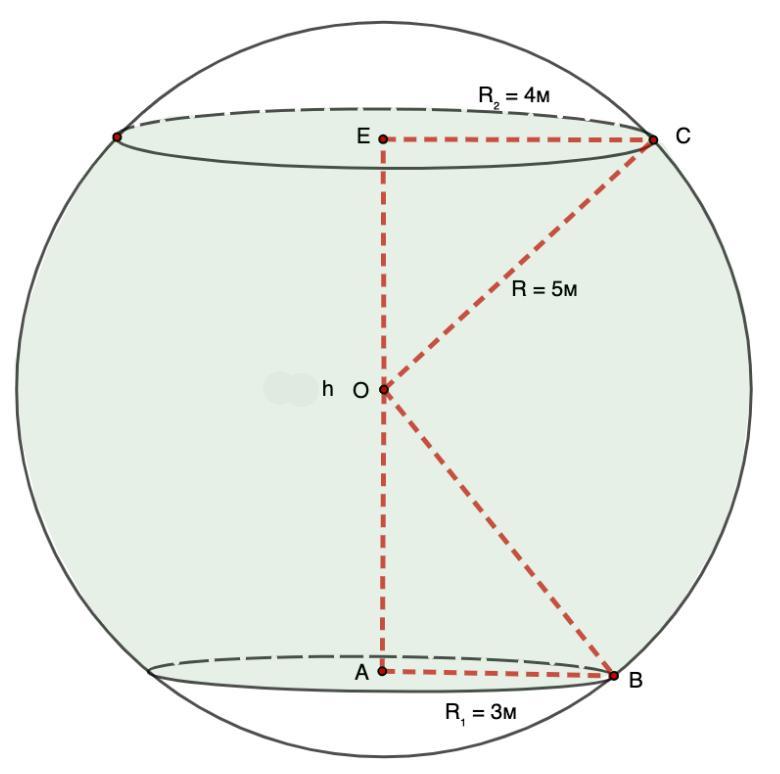
2. Основания шарового слоя лежат по разные стороны от центра шара.
Тогда h = AE = AO + OE = 4 + 3 = 7 (м)
Найдем объем: