Question

Терміноооовоооо!!!! 100б


Сторона правильного трикутника, вписаного в коло дорівнює 5корінь 3 см. Знайдіть сторону правильного шестикутника, описаного навколо нього кола.

Answer 1

Ответ:

Сторона правильного шестикутника, описаного навколо нього кола дорівнює $\dfrac{10\sqrt{3} }{3}$ см

Объяснение:

Сторона правильного трикутника, вписаного в коло дорівнює 5корінь 3 см. Знайдіть сторону правильного шестикутника, описаного навколо нього кола.

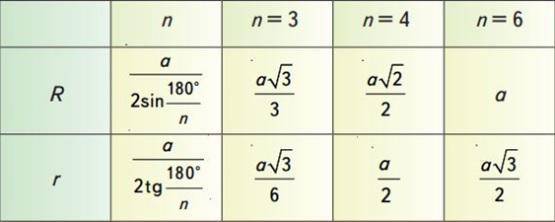
Формули для обчислення радіуса кола r, вписаного в правильний многокутник, та  радіуса кола R, описаного навколо правильного многокутника, дивись у таблиці.

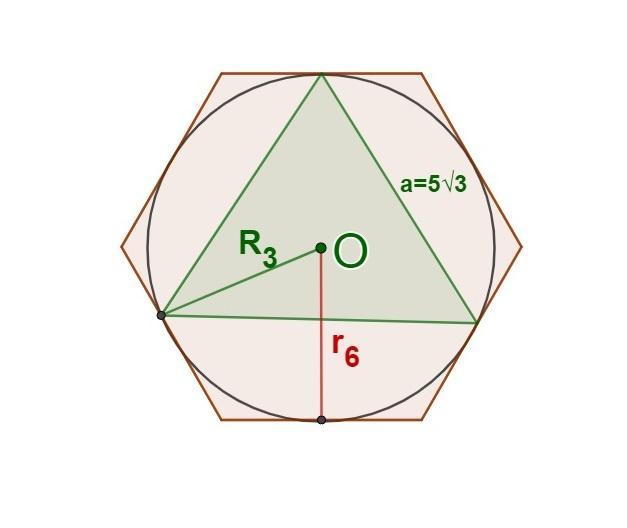
1) За умовою, сторона  правильного трикутника, вписаного в коло дорівнює а₃=5√3 см.

Тоді знайдемо радіус  R₃, описаного навколо правильного трикутника кола:

$\bf R_3=\dfrac{a_3\sqrt{3} }{3}$

$\sf R_3=\dfrac{5\sqrt{3}\cdot \sqrt{3} }{3}=\bf 5$  (см)

2) Радіус кола, описаного навколо правильного трикутника є також рідіусом кола,  вписаного в правильний шестікутник:

r₆=R₃=5 (см)

3) Радіус  r₆, вписаного в правильний шестікутник кола:

$\bf r_6=\dfrac{a_6\sqrt{3} }{2}$

Тоді сторона правильного шестікутника буде дорівнювати:

$\sf a_6=\dfrac{2\sqrt{3}\cdot r_6}{3} =\dfrac{2\sqrt{3}\cdot5}{3} =\bf \dfrac{10\sqrt{3} }{3}$   (cм)

Відповідь: $\dfrac{10\sqrt{3} }{3}$  (см)