Question

#СТОБАЛЛОВ ОЧЕНЬ СРОЧНО За СПАМ БАН. На основании равностороннего треугольника как на диаметре построена полуокружность, рассекающая треугольник на две части. Сторона треугольника равна $\sqrt{\frac{3}{3\sqrt{3}-\pi }}$.‍ Найдите площадь той части треугольника, которая лежит вне круга. Ответ запишите десятичной дробью.

Answer 1

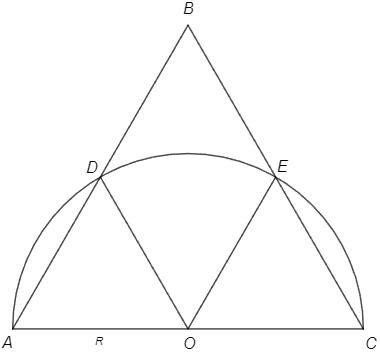
Пусть сторона большого треугольника 2R.

△AOD - р/б с углом 60 - равносторонний, AD=R =DB

Аналогично BE=R

ODBE - ромб с углом 60

Искомая площадь = ромб с углом 60 минус сектор с углом 60

S =R^2 √3/2 - пR^2/6 =R^2 (3√3-п)/6

2R=√(3/(3√2-п)) => R^2 =3/4(3√3-п)

S =3/4(3√3-п) *(3√3-п)/6 =1/8 =0.125