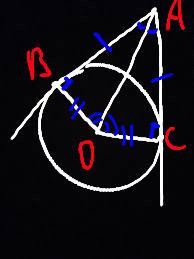
Через точки В і С, що лежать на колі з центром у точці О, проведено дотичні АВ і АС. Довести, що АО бісектриса кута Намалювати рисунок якщо потрібен
Ответы
Ответ дал:
1
Відповідь:
Дано: коло з центром О, АВ і АС - дотичні, В і С - точки дотику.
Довести: АО - бісектриса кута.
Доведення:
AB = AC за властивістю дотичних. OB = OC = R. трикутник ОАВ = трикутник ОАС за трьома сторонами (АВ = АС, ОВ = ОС, ОА, спільна сторона).
кут ВАО = кут САО за властивістю рівних кутів, звідси маємо що АО бісектриса кута ВАС.
Відповідь: АО - бісектриса. Доведено.
Пояснення:
Всі пояснення є у відповіді.
Приложения:
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад