Question

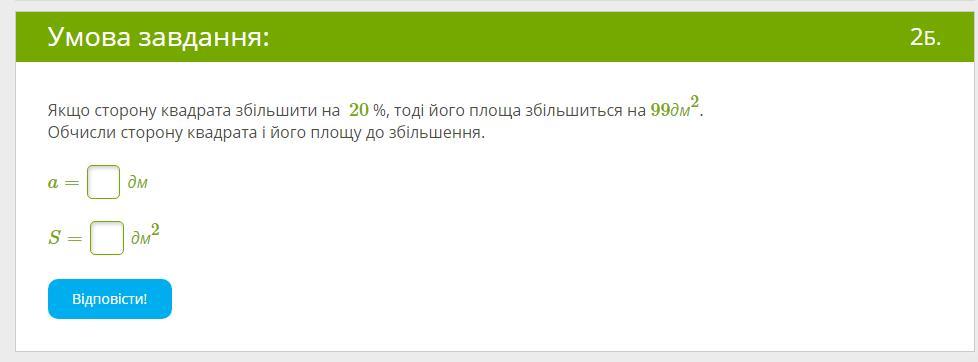
Якщо сторону квадрата збільшити на 20 %, тоді його площа збільшиться на 99дм2.
Обчисли сторону квадрата і його площу до збільшення.

Answer 1

Ответ:

Нехай x - довжина сторони квадрата до збільшення.

Згідно умови, якщо сторону квадрата збільшити на 20%, то вона становитиме 1.2x (120% від x).

Далі, знайдемо площу квадрата до збільшення:

площа = x^2

Знайдемо площу квадрата після збільшення:

площа + 99 = (1.2x)^2 = 1.44x^2

Запишемо рівняння за умовою:

1.44x^2 = x^2 + 99

Розв'яжемо його:

0.44x^2 = 99

x^2 = 99 / 0.44

x^2 ≈ 225

x ≈ 15

Отже, сторона квадрата до збільшення становила 15 дм, а його площа дорівнювала 225 дм^2.

Після збільшення, сторона квадрата становитиме 1.2 * 15 = 18 дм, а його площа буде дорівнювати 1.44 * 225 = 324 дм^2.