Question

Обчислити подвійний інтеграл, переходячи до полярних або до узагальнено полярних координат:

Answer 1

Решение.

Формулы перехода к полярным координатам :  

  $\bf x=r\, cos\varphi \ \ ,\ \ y=r\ sin\varphi \ \ ,\ \ dx\, dy=r\, dr\, d\varphi$

 

$\bf x^2+y^2=9\ \ \ \Rightarrow \ \ r^2cos^2\varphi +r^2sin^2\varphi =9\ \ \Rightarrow \ \ r=3\\\\x^2+y^2=16\ \ \Rightarrow \ \ \ r=4\\\\x\geq 0\ \ \Rightarrow \ \ \ r\, cos\varphi \geq 0\ \ ,\ \ cos\varphi \geq 0\ \ ,\ \ -\dfrac{\pi }{2}\leq \varphi \leq \dfrac{\pi }{2}$

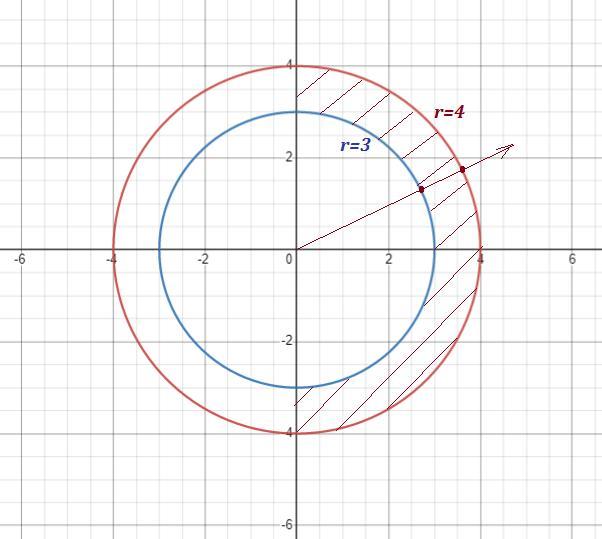
Область интегрирования - полукольцо, расположенное в 1 и 4 четвертях .    

$\bf \displaystyle \iint\limits_{D}\, \sqrt{x^2+y^2-9}\, dx\, dy=\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}d\varphi \int\limits_{3}^{4}\, \sqrt{r^2-9}\cdot r\, dr=\\\\\\=\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}d\varphi \int\limits_{3}^{4}\, \frac{1}{2}\sqrt{r^2-9}\cdot d(r^2-9)=\frac{1}{2}\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}\left(\frac{\sqrt{(r^2-9)^3}}{3/2}\, \Big|_3^4\right)d\varphi =$  

$\bf \displaystyle =\frac{1}{2}\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}\left(\frac{2\sqrt{(16-9)^3}}{3}-0\, \right)d\varphi =\frac{\sqrt{7^3}}{3}\int\limits_{-\frac{\pi }{2}}^{\frac{\pi }{2}}\, d\varphi=\frac{7\sqrt7}{3}\cdot \varphi \, \Big|_{-\frac{\pi }{2}}^{\frac{\pi }{2}}=\\\\\\=\boldsymbol{\frac{7\sqrt7}{3}\cdot \Big(\frac{\pi }{2}+\frac{\pi}{2}\Big)=\frac{7\sqrt7}{3}\cdot \pi }$