Question

В сферу радиуса R вписана правильная треугольная пирамида с плоским углом при вершине грани a.Вычислить объем этой пирамиды.

Answer 1

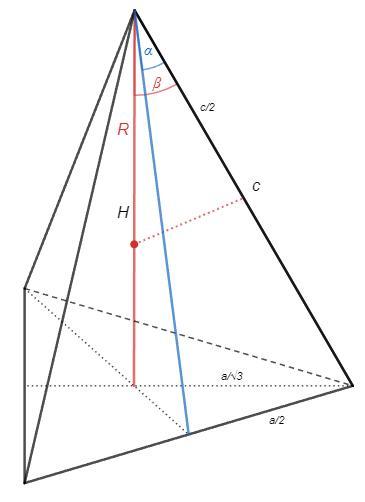
Центр описанной сферы лежит на высоте пирамиды и на серединном перпендикуляре к боковой стороне.

Н - высота

с - боковая сторона

a - сторона основания

A - угол между боковой стороной и апофемой (альфа=2A)

B - угол между боковой стороной и высотой

sinB =2/√3 sinA

cosB^2 =1-sinB^2 =1 -4/3 sinA^2

c/2R =H/c =cosB

H =2R cosB^2

c^2 =2RH

a/2 =c sinA => a^2 =8 RH sinA^2

So =√3/4 a^2 =2√3 RH sinA^2

Собираем ответ:

V =1/3 So H

=2/√3 RH^2 sinA^2

=2/√3 R [ 4R^2 (3-4sinA^2)^2 /9 ] sinA^2

=8/9√3 R^3 sinA^2 (3-4sinA^2)^2

Ответ:

$V = \frac{8}{9\sqrt{3}} R^3 sin^2\frac{\alpha}{2} (3-4sin^2\frac{\alpha}{2})^2$