Question

В треугольнике ABC стороны AB=17; ВС=12; АС=20. Найдите наибольший угол треугольника. ​

Answer 1

Відповідь:

∠B

Пояснення:

Напроти найбільшої сторони лежить найбільший кут, і навпаки.

Answer 2

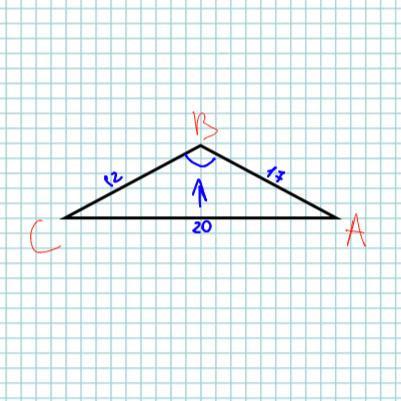
Против большей стороны лежит больший угол .

Против стороны AC лежит больший угол B .

Запишем теорему косинусов для стороны AC и найдём < B .

$\displaystyle\bf\\AC^{2} =AB^{2} +BC^{2} -2\cdot AB \cdot BC \cdot Cos < B\\\\20^{2} =17^{2} +12^{2} -2\cdot 17\cdot 12\cdot Cos < B\\\\408Cos < B=289+144-400\\\\408Cos < B=33\\\\Cos < B=\frac{33}{408} =\frac{11}{136} \\\\\\ < B=arcCos\frac{11}{136}$