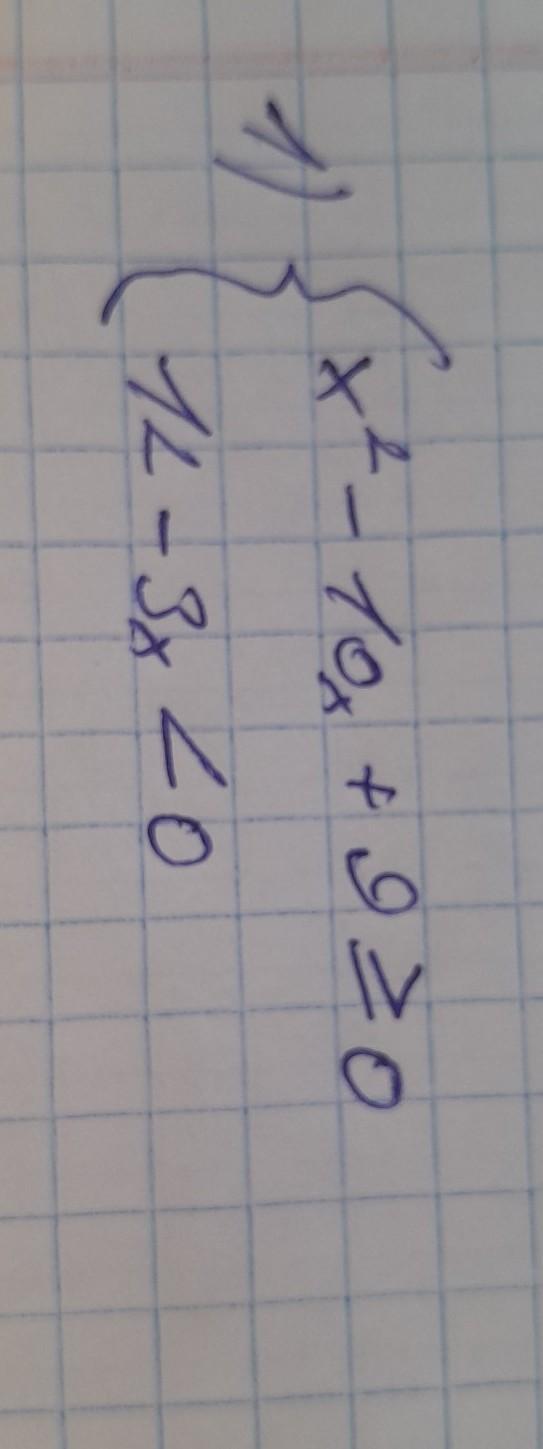Ответы
Ответ дал:
1
Объяснение:
Решение системы неравенств:
x²-10x+9 ≥ 0
Для решения этого неравенства найдем корни квадратного трехчлена x²-10x+9=0:
x₁=1, x₂=9.
Построим график функции y=x²-10x+9:
Видим, что функция равна нулю в точках x=1 и x=9, и является положительной на промежутках (-∞, 1) и (9, +∞), а отрицательной на промежутке (1, 9).
Таким образом, неравенство x²-10x+9 ≥ 0 выполняется на промежутках (-∞, 1] и [9, +∞).
12-3x < 0
Перенесем переменную на одну сторону и получим:
-3x < -12
Разделим обе части неравенства на -3, помня, что при делении на отрицательное число меняется знак неравенства:
x > 4
Таким образом, система неравенств имеет решение на промежутке (4, +∞).
Ответ: x > 4.
Вас заинтересует
1 год назад
1 год назад
1 год назад
1 год назад
3 года назад
3 года назад
8 лет назад
8 лет назад