Question

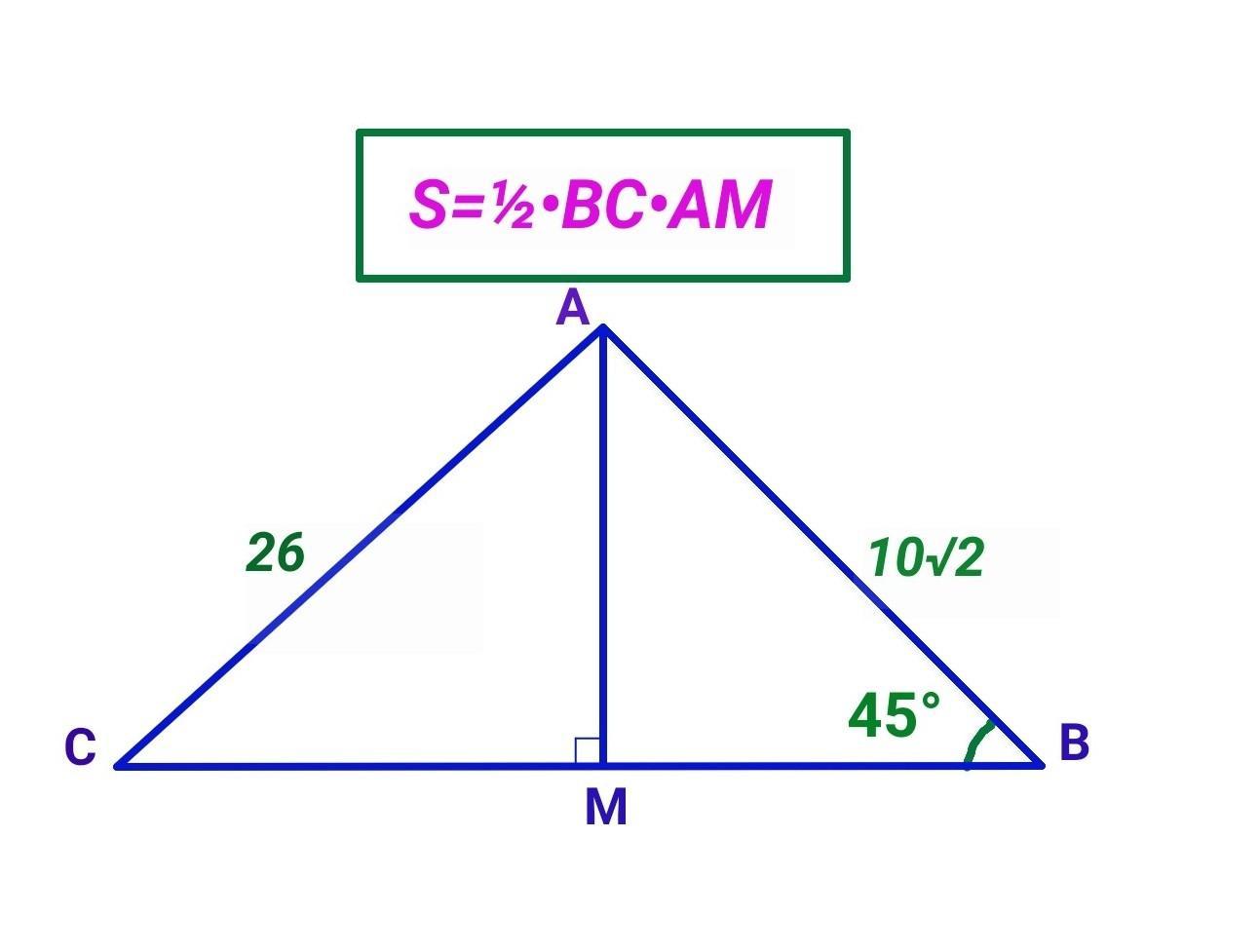
Висота АМ трикутника АВС ділить його сторону ВС на відрізки ВМ і МС. Знайдіть площу трикутника АВС якщо АВ = 10√2 см, АС = 26 см , кут В =45. C нормальним об'ясненням. ДУЖЕ ТРЕБА!!!!!!!!!!

Answer 1

Ответ:

Площа трикутника дорівнює 170 см²

Объяснение:

Висота АМ трикутника АВС ділить його сторону ВС на відрізки ВМ і МС. Знайдіть площу трикутника АВС якщо АВ = 10√2 см, АС = 26 см , кут В =45°.

• Площа трикутника дорівнює половині добутку сторони на висоту, проведену до неї.

Нехай АВС - даний трикутник, АМ⟂ВС, АВ = 10√2 см, АС = 26 см , ∠В =45°.

1) Розглянемо прямокутний трикутник АМВ(∠АМВ=90°)

За означенням косинуса гострого кута прямокутного трикутника маємо:

$cos\angle B = \dfrac{MB}{AB} \\ \\ cos 45^\circ = \dfrac{MB}{10 \sqrt{2} } \\ \\ \frac{ \sqrt{2} }{2} = \frac{MB}{10 \sqrt{2} }$

$MB = \dfrac{10 \sqrt{2} \times \sqrt{2} }{2} = \bf 10(см)$

За теоремою про суму кутів прямокутного трикутника знайдемо кут МАВ:

∠МАВ=90°-∠В=90°-45°=45°

Так як ∠МАВ=∠В, то △АМВ - рівнобедрений з основою АВ, отже:

АМ=МВ=10(см) - як бічні сторони рівнобедреного трикутника

2) Розглянемо прямокутний трикутник АМС(∠АМС=90°).

За теоремою Піфагора знайдемо катет СМ:

$CM = \sqrt{ {AC }^{2} - {AM}^{2} } = \sqrt{ {26}^{2} - {10}^{2} } = \\ \\ = \sqrt{(26 - 10)(26 + 10)} = \sqrt{16 \times 36} = 4 \times 6 = \bf 24(cm)$

3) За аксиомою вимірювання відрізків отримаємо:

ВС=МВ+СМ=10+24=34(см)

4) Площа трикутника АВС:

S=½•BC•AM

S=½•34•10=170 (см²)

Відповідь: 170 см²