Відрізки AB i CD - діаметри одного кола. Площина a не має спільних точок з даним колом. через точки A, B, C i D провели паралельні прямі які перетинають площину a відповідно в точках A1, B1, C1 i D1. Знайдіть відрізок CC1, якщо AA1 = 5 см BB1 = 9 см DD1 = 3 см
Ответы
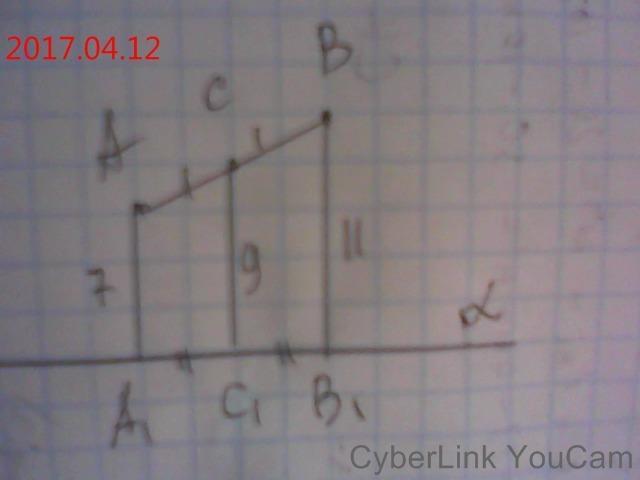
см фото.
α -площина, за умовою: АА1=7 см и АА1⊥α; ВВ1=11 см и ВВ1⊥α;
СС1 ⊥α, АС=ВС.
АА1 ║ ВВ1 ║СС1,
СС1 - середня лінія трапеції
отже, СС1=(7+11)/2=9 см.
Відповідь: 9 см.
Ответ:
В даній задачі ми маємо коло з діаметрами AB і CD, і площину a, яка не має спільних точок з цим колом. Через точки A, B, C і D проведені паралельні прямі, які перетинають площину a в точках A1, B1, C1 і D1. Ми знаємо, що довжини відрізків AA1, BB1 і DD1 дорівнюють відповідно 5 см, 9 см і 3 см.
Оскільки відрізки AB і CD є діаметрами кола, то точки A, B, C і D лежать на колі, і ці діаметри перпендикулярні між собою. Отже, ми можемо вважати, що відрізки A1B1 і C1D1 також є діаметрами цього кола, оскільки вони паралельні діаметрам AB і CD і також перпендикулярні до площини a.
Знайдемо відрізок CC1. Оскільки AB і C1D1 є діаметрами кола, то вони проходять через центр кола, і їх перетин буде центром кола. Позначимо центр кола як O.
Таким чином, відрізок CC1 є діаметром кола і має довжину, рівну діаметру кола.
Тепер ми маємо інформацію про довжини відрізків AA1, BB1 і DD1, але нам необхідно знайти довжину відрізка CC1. Оскільки A1B1 і C1D1 є паралельними, ми можемо вважати, що вони подібні за співвідношенням сторін, оскільки вони мають паралельні сторони.
Запишемо співвідношення між довжинами відрізків:
AA1 : CC1 = BB1 : DD1
Підставимо відомі значення:
5 : CC1 = 9 : 3
5 : CC1 = 3
Тепер розв'яжемо рівняння відносно CC1:
CC1 = 5 / 3
Отже, довжина відрізка CC1 дорівнює 5/3 см
Пошаговое объяснение: